A day full of math games & activities. Find one near you.
A day full of math games & activities. Find one near you.
A day full of math games & activities. Find one near you.
A day full of math games & activities. Find one near you.
LearnPracticeDownload

Trigonometric Equations

The trigonometric equations involve trigonometric functions of angles as variables. The angle of θ trigonometric functions such as Sinθ, Cosθ, Tanθ is used as a variable in trigonometric equations. Similar to general polynomial equations, the trigonometric equations also have solutions, which are referred to as principal solutions, and general solutions.

We will use the fact that the period of sin x and cos x is 2π and the period of tan x is π to find the solutions of the trigonometric equations. Let us learn more about trigonometric equations, the method to solve them, and find their solutions with the help of a few solved examples of trigonometric equations for a better understanding of the concept.

1. What are Trigonometric Equations?
2. Trigonometric Equations Formulas   
3. Solving Trigonometric Equations
4. Steps to Solve Trigonometric Equations
5. Examples of Solving Trigonometric Equations
6. FAQs on Trigonometric Equations

What are Trigonometric Equations?

The trigonometric equations are similar to algebraic equations and can be linear equations, quadratic equations, or polynomial equations. In trigonometric equations, the trigonometric ratios of Sinθ, Cosθ, Tanθ are represented in place of the variables, as in a normal polynomial equation. The trigonometric ratios used in trigonometric equations are Sinθ, Cosθ, or Tanθ.

The linear equation ax + b = 0 can be written as a trigonometry equation as aSinθ + b = 0, which is also sometimes written as Sinθ = Sinα. The quadratic equation ax2 + bx + c = 0 is as an example of trigonometric equation is written as aCos2θ + bCosθ + c = 0. But unlike normal solutions of equations with the number of solutions based on the degree of the variable, in trigonometric equations, the same value of solution exists for different values of θ. For example, we have Sinθ = 1/2 = Sinπ/6 = Sin5π/6 = Sin13π/6, and so on as the values of the sine function repeat after every 2π radians.

Some of the examples of trigonometric equations are as follows.

  • Sin2x - Sin4x + Sin6x = 0
  • 2Cos2x + 3Sinx = 0
  • Cos4x = Cos2x
  • Sin2x + Cosx = 0
  • Sec22x = 1 - Tan2x

Trigonometric Equations Formulas

We use some results and general solutions of the basic trigonometric equations to solve other trigonometric equations. These results are as follows:

  • For any real numbers x and y, sin x = sin y implies x = nπ + (-1)ny, where n ∈ Z.
  • For any real numbers x and y, cos x = cos y implies x = 2nπ ± y, where n ∈ Z.
  • If x and y are not odd multiples of π/2, then tan x = tan y implies x = nπ + y, where n ∈ Z.

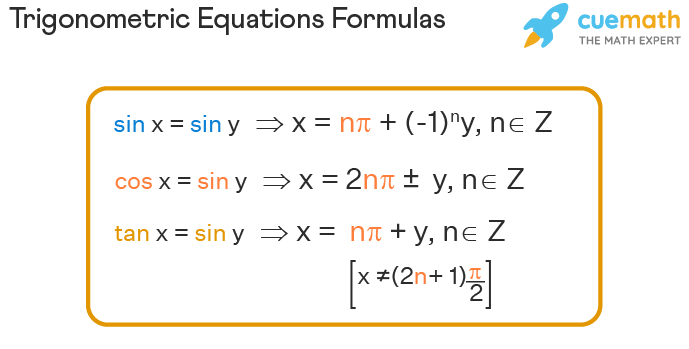
Trigonometric Equations

Now, we can prove these results using trigonometric formulas.

Prove that for any real numbers x and y, sin x = sin y implies x = nπ + (-1)ny, where n ∈ Z

Proof: If sin x = sin y, then sin x – sin y = 0

⇒ 2 cos (x + y)/2 sin (x − y)/2 = 0 --- [Using formula Sin A - Sin B = 2 cos ½ (A + B) sin ½ (A - B)]

⇒ cos (x + y)/2 = 0 or sin (x − y)/2 = 0

⇒ (x + y)/2 = (2n + 1)π /2 or (x − y)/2 = nπ, where n ∈ Z ---- [Because sin A = 0 implies A = nπ and cos A = 0 implies A = (2n + 1)π/2, where n ∈ Z]

i.e. x = (2n + 1) π – y or x = 2nπ + y, where n ∈ Z.

Hence x = (2n + 1)π + (–1)2n + 1y or x = 2nπ + (–1)2n y, where n ∈ Z.

Combining these two results, we get x = nπ + (–1)ny, where n ∈ Z.

Prove that for any real numbers x and y, cos x = cos y implies x = 2nπ ± y, where n ∈ Z.

Proof: If cos x = cos y, then cos x – cos y = 0

⇒ -2 sin (x + y)/2 sin (x − y)/2 = 0 --- [Using formula Cos A - Cos B = - 2 sin ½ (A + B) sin ½ (A - B)]

⇒ sin (x + y)/2 = 0 or sin (x − y)/2 = 0

⇒ (x + y)/2 = nπ or (x − y)/2 = nπ, where n ∈ Z ---- [Because sin A = 0 implies A = nπ, where n ∈ Z]

i.e. x = 2nπ – y or x = 2nπ + y, where n ∈ Z.

Hence x = 2nπ ± y, where n ∈ Z.

Prove that if x and y are not odd multiples of π/2, then tan x = tan y implies x = nπ + y, where n ∈ Z.

Proof: If tan x = tan y, then tan x - tan y = 0

⇒ sin x / cos x - sin y / cos y = 0

⇒ (sin x cos y - cos x sin y) / (cos x cos y) = 0

⇒ sin (x - y) / (cos x cos y) = 0 ---- [Using trigonometric formula sin (A - B) = sinA cosB - sinB cosA]

⇒ sin (x - y) = 0

⇒ x - y = nπ, where n ∈ Z --- [Because sin A = 0 implies A = nπ, where n ∈ Z]

⇒ x = nπ + y, where n ∈ Z

Solving Trigonometric Equations

Unlike normal solutions of algebraic equations with the number of solutions based on the degree of the variable, in trigonometric equations, the solutions are of two types, based on the different value of angle for the trigonometric function, for the same solution. For example, for a simple trigonometric equation 2Cosθ - 1 = 0, the solution is given by, Cosθ = 1/2 and, the θ values are π/3, 5π/3, 7π/3, 11π/3, and so on as the values of the cosine function repeat after every 2π radians and cos x is positive in the first and fourth quadrants. We have two types of solutions to the trigonometric equations:

  • Principal Solution: The initial values of angles for the trigonometric functions are referred to as principal solutions. The solution of Sinx and Cosx repeat after an interval of 2π, and the solution of Tanx repeat after an interval of π. The solutions of these trigonometric equations, for which x lies between 0 and 2π, are called principal solutions.
  • General Solution: The values of the angles for the same answer of the trigonometric function are referred to as the general solution of the trigonometric function. The solutions of trigonometric equations beyond 2π are all consolidated and expressed as a general solution of the trigonometric equations. The general solutions of Sinθ, Cosθ, Tanθ are as follows.
    • Sinθ = Sinα, and the general solution is θ = nπ + (-1)nα, where n ∈ Z
    • Cosθ = Cosα, and the general solution is θ = 2nπ + α, where n ∈ Z
    • Tanθ = Tanα, and the general solution is θ = nπ + α, where n ∈ Z

Steps to Solve Trigonometric Equations

The following steps are to be followed, for solving a trigonometric equation.

  • Transform the given trigonometric equation into an equation with a single trigonometric ratio (sin, cos, tan)
  • Change the equation with the trigonometric equation, having multiple angles, or submultiple angles into a simple angle.
  • Now represent the equation as a polynomial equation, quadratic equation, or linear equation.
  • Solve the trigonometric equation similar to normal equations, and find the value of the trigonometric ratio.
  • The angle of the trigonometric ratio or the value of the trigonometric ratio represents the solution of the trigonometric equation.

Examples of Solving Trigonometric Equations

Example 1: Find the principal solutions of the trigonometric equation sin x = √3/2.

Solution: To find the principal solutions of sin x = √3/2, we know that sin π/3 = √3/2 and sin (π - π/3) = √3/2

⇒ sin π/3 = sin 2π/3 = √3/2

We can find other values of x such that sin x = √3/2, but we need to find only those values of x such that x lies in [0, 2π] because a principal solution lies between 0 and 2π.

So, the principal solutions of sin x = √3/2 are x = π/3 and 2π/3.

Example 2: Find the solution of cos x = 1/2.

Solution: In this case, we will find the general solution of cos x = 1/2. We know that cos π/3 = 1/2, so we have

cos x = 1/2

⇒ cos x = cos π/3

⇒ x = 2nπ + (π/3), where n ∈ Z ---- [Using Cosθ = Cosα, and the general solution is θ = 2nπ + α, where n ∈ Z]

Therefore, the general solution of cos x = 1/2 is x = 2nπ + (π/3), where n ∈ Z.

Important Notes on Trigonometric Equations

  • For any real numbers x and y, sin x = sin y implies x = nπ + (-1)ny, where n ∈ Z.
  • For any real numbers x and y, cos x = cos y implies x = 2nπ ± y, where n ∈ Z.
  • If x and y are not odd multiples of π/2, then tan x = tan y implies x = nπ + y, where n ∈ Z.
  • sin A = 0 implies A = nπ and cos A = 0 implies A = (2n + 1)π/2, where n ∈ Z

Related Topics

 

Trigonometric Equations Examples

  1. Example 1: Find the principal solution of the trigonometric equation tan x = -√3

    Solution: Here we have tan x = -√3, and we know that tan π/3 = √3. So, we have

    tan x = -√3

    ⇒ tan x = - tan π/3

    ⇒ tan x = tan(π - π/3) OR tan x = tan(2π - π/3)

    ⇒ tan x = tan 2π/3 OR tan x = tan 5π/3.

    Therefore, the principal solutions of tan x = -√3 are 2π/3 and 5π/3

    Answer: Principal solutions are x = 2π/3 and x = 5π/3.

  2. Example 2: Find the general solution of the trigonometric equation 2 cos2x + 3 sin x = 0.

    Solution: The given trigonometric equation is 2 cos2x + 3 sin x = 0.

    ⇒ 2(1 - sin2x) + 3 sin x = 0 --- [Using trigonometric formula cos2x + sin2x = 1 which implies cos2x = 1 - sin2x]

    ⇒ 2 - 2 sin2x + 3 sin x = 0

    ⇒ 2 sin2x - 3 sin x - 2 = 0

    ⇒ 2sin2x - 4 sin x + sin x - 2 = 0

    ⇒ 2 sin x(sin x - 2) + 1(sin x - 2) = 0

    ⇒ (2sin x + 1)(sin x - 2) = 0

    ⇒ 2 sin x + 1 = 0, sin x - 2 = 0

    ⇒ sin x = -1/2 or sin x = 2

    ⇒ sin x = 2 is not defined since the values of sin x lies between -1 and +1.

    So, we have sin x = -1/2. We know that sin π/6 = 1/2.

    sin x = -1/2

    ⇒ sin x = - sin (π/6)

    ⇒ sin x = sin (-π/6)

    = sin (π + π/6)

    = sin (7π/6)

    Therefore, we have x = nπ + (-1)n(7π/6), where n ∈ Z --- [Because for any real numbers x and y, sin x = sin y implies x = nπ + (-1)ny, where n ∈ Z.]

    Answer: General solution of the above trigonometric equation is nπ +(-1)n(7π/6), where n ∈ Z

  3. Example 3: Solve sin 2x – sin 4x + sin 6x = 0.

    Solution: The equation sin 6x + sin 2x − sin 4x = 0 can be written as

    2 sin 4x cos2x − sin 4x = 0 --- [Using sin A + sin B = 2 sin (A + B)/2 cos (A - B)/2]

    ⇒ sin 4x(2 cos2x − 1) = 0

    ⇒ sin 4x = 0 or 2 cos2x - 1 = 0

    ⇒ 4x = nπ or cos 2x = 1/2, , where n ∈ Z

    ⇒ 4x = nπ or cos 2x = cos π/3 --- [Because cos π/3 = 1/2], , where n ∈ Z

    ⇒ x = nπ/4 or 2x = 2nπ ± (π/3), , where n ∈ Z

    ⇒ x = nπ/4 or x = nπ ± (π/6), , where n ∈ Z

    Answer: The generla solution is x = nπ/4 or x = nπ ± (π/6).

View Answer >

go to slidego to slidego to slide

Breakdown tough concepts through simple visuals.
Math will no longer be a tough subject, especially when you understand the concepts through visualizations.

Book a Free Trial Class

FAQs on Trigonometric Equations

What are Trigonometric Equations?

The trigonometric equations are similar to algebraic equations and can be linear equations, quadratic equations, or polynomial equations. In trigonometric equations, the trigonometric ratios of Sinθ, Cosθ, Tanθ are represented in place of the variables.

What are the Three Trigonometric Equations Formulas?

The three trigonometric equations are based on the three trigonometric functions. The three trigonometric equations are Sinθ = Sinα, Cosθ = Cosα, Tanθ = Tanα. The three trigonometric equations formulas are as follows:

  • For any real numbers x and y, sin x = sin y implies x = nπ + (-1)ny, where n ∈ Z.
  • For any real numbers x and y, cos x = cos y implies x = 2nπ ± y, where n ∈ Z.
  • If x and y are not odd multiples of π/2, then tan x = tan y implies x = nπ + y, where n ∈ Z.

Give Trigonometric Equations Examples.

Some of the examples of trigonometric equations are as follows:

  • Sin2x - Sin4x + Sin6x = 0
  • 2Cos2x + 3Sinx = 0
  • Cos4x = Cos2x

What are the Steps to Solve Trigonometric Equations?

The following steps are helpful for solving a trigonometric equation:

  • Transform the given trigonometric equation into an equation with a single trigonometric ratio.
  • Change the equation with the trigonometric equation, having multiple angles, or submultiple angles into a simple. angle.
  • Now represent the equation as a polynomial equation, quadratic equation, or linear equation.
  • Solve the trigonometric equation similar to normal equations, and find the value of the trigonometric ratio.
  • The angle of the trigonometric ratio or the value of the trigonometric ratio represents the solution of the trigonometric equation.

What is the Difference Between Trigonometric Equations and Algebraic Equations?

The trigonometric equation and the algebraic equations differ in the variable used for the equation. In a trigonometric equation, the trigonometric function is the variable, and in an algebra the alphabets x, y are taken as variables. Both the trigonometric equations and algebraic equations have linear equations, quadratic equations, and polynomial equations.

What is the Difference Between Trigonometric Equations and Identities?

Trigonometric Equations are like algebraic equations where we are required to determine the solution and find the value of the variable. On the other hand, trigonometric identities are results in trigonometry that express the relationship between different trigonometric ratios.

What is the Principal Solution of Trigonometric Equations?

we know that sin x and cos x repeat after every 2π radians and tan x repeat after every π radians. The solutions of a trigonometric equation for which 0 ≤ x < 2π are called principal solutions.

How to Find the General Solution of Trigonometric Equations?

We can find the general solution of trigonometric equations using the following three results:

  • For any real numbers x and y, sin x = sin y, implies x = nπ + (-1)ny, where n ∈ Z.
  • For any real numbers x and y, cos x = cos y, implies x = 2nπ ± y, where n ∈ Z.
  • If x and y are not odd multiples of π/2, then tan x = tan y implies x = nπ + y, where n ∈ Z.
Download FREE Study Materials
Trigonometric Equations Worksheet
Math worksheets and
visual curriculum