Tan 11pi/12
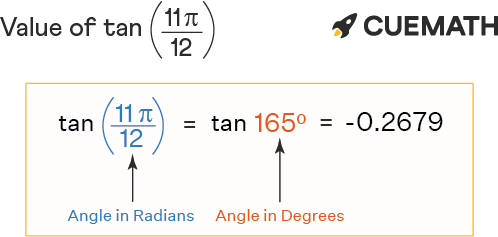
The value of tan 11pi/12 is -0.2679491. . .. Tan 11pi/12 radians in degrees is written as tan ((11π/12) × 180°/π), i.e., tan (165°). In this article, we will discuss the methods to find the value of tan 11pi/12 with examples.
- Tan 11pi/12: -2 + √3
- Tan 11pi/12 in decimal: -0.2679491. . .
- Tan (-11pi/12): 0.2679491. . . or 2 - √3
- Tan 11pi/12 in degrees: tan (165°)
What is the Value of Tan 11pi/12?
The value of tan 11pi/12 in decimal is -0.267949192. . .. Tan 11pi/12 can also be expressed using the equivalent of the given angle (11pi/12) in degrees (165°).
We know, using radian to degree conversion, θ in degrees = θ in radians × (180°/pi)
⇒ 11pi/12 radians = 11pi/12 × (180°/pi) = 165° or 165 degrees
∴ tan 11pi/12 = tan 11π/12 = tan(165°) = -2 + √3 or -0.2679491. . .
Explanation:
For tan 11pi/12, the angle 11pi/12 lies between pi/2 and pi (Second Quadrant). Since tangent function is negative in the second quadrant, thus tan 11pi/12 value = -2 + √3 or -0.2679491. . .
Since the tangent function is a periodic function, we can represent tan 11pi/12 as, tan 11pi/12 = tan(11pi/12 + n × pi), n ∈ Z.
⇒ tan 11pi/12 = tan 23pi/12 = tan 35pi/12 , and so on.
Note: Since, tangent is an odd function, the value of tan(-11pi/12) = -tan(11pi/12).
Methods to Find Value of Tan 11pi/12
The tangent function is negative in the 2nd quadrant. The value of tan 11pi/12 is given as -0.26794. . .. We can find the value of tan 11pi/12 by:
- Using Unit Circle
- Using Trigonometric Functions
Tan 11pi/12 Using Unit Circle
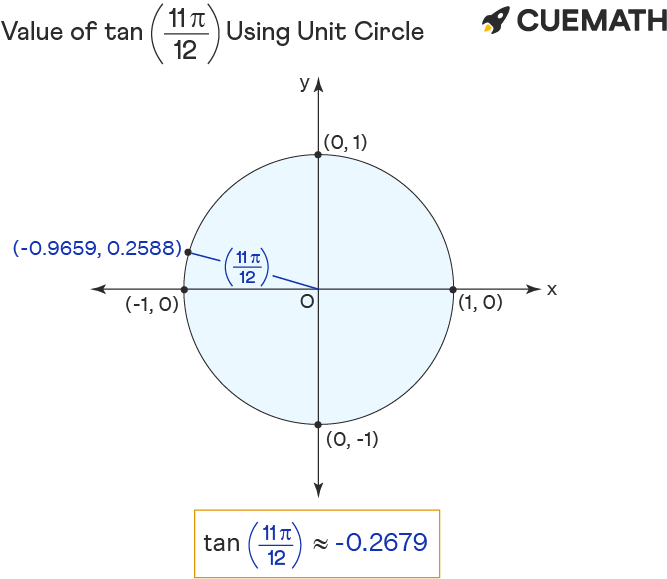
To find the value of tan 11π/12 using the unit circle:
- Rotate ‘r’ anticlockwise to form 11pi/12 angle with the positive x-axis.
- The tan of 11pi/12 equals the y-coordinate(0.2588) divided by the x-coordinate(-0.9659) of the point of intersection (-0.9659, 0.2588) of unit circle and r.
Hence the value of tan 11pi/12 = y/x = -0.2679 (approx)
Tan 11pi/12 in Terms of Trigonometric Functions
Using trigonometry formulas, we can represent the tan 11pi/12 as:
- sin(11pi/12)/cos(11pi/12)
- ± sin(11pi/12)/√(1 - sin²(11pi/12))
- ± √(1 - cos²(11pi/12))/cos(11pi/12)
- ± 1/√(cosec²(11pi/12) - 1)
- ± √(sec²(11pi/12) - 1)
- 1/cot(11pi/12)
Note: Since 11pi/12 lies in the 2nd Quadrant, the final value of tan 11pi/12 will be negative.
We can use trigonometric identities to represent tan 11pi/12 as,
- cot(pi/2 - 11pi/12) = cot(-5pi/12)
- -cot(pi/2 + 11pi/12) = -cot 17pi/12
- -tan (pi - 11pi/12) = -tan pi/12
☛ Also Check:
FAQs on Tan 11pi/12
What is Tan 11pi/12?
Tan 11pi/12 is the value of tangent trigonometric function for an angle equal to 11π/12 radians. The value of tan 11pi/12 is -2 + √3 or -0.2679 (approx).
What is the Value of Tan 11pi/12 in Terms of Cos 11pi/12?
We know, using trig identities, we can write tan 11pi/12 as √(1 - cos²(11pi/12))/cos 11pi/12. Here, the value of cos 11pi/12 is equal to -0.965925.
What is the Value of Tan 11pi/12 in Terms of Cosec 11pi/12?
Since the tangent function can be represented using the cosecant function, we can write tan 11pi/12 as -1/√(cosec²(11pi/12) - 1). The value of cosec 11pi/12 is equal to 3.86370.
How to Find the Value of Tan 11pi/12?
The value of tan 11pi/12 can be calculated by constructing an angle of 11π/12 radians with the x-axis, and then finding the coordinates of the corresponding point (-0.9659, 0.2588) on the unit circle. The value of tan 11pi/12 is equal to the y-coordinate(0.2588) divided by the x-coordinate (-0.9659). ∴ tan 11pi/12 = -2 + √3 or -0.2679
How to Find Tan 11pi/12 in Terms of Other Trigonometric Functions?
Using trigonometry formula, the value of tan 11pi/12 can be given in terms of other trigonometric functions as:
- sin(11pi/12)/cos(11pi/12)
- ± sin(11pi/12)/√(1 - sin²(11pi/12))
- ± √(1 - cos²(11pi/12))/cos(11pi/12)
- ± 1/√(cosec²(11pi/12) - 1)
- ± √(sec²(11pi/12) - 1)
- 1/cot(11pi/12)
☛ Also check: trigonometric table