Sin of 2pi
Before going to find the value of sin of 2pi, let us recollect the values of sine function of different standard angles from the trigonometric table. sin 0 = 0, sin π/6 = 1/2, sin π/4 = √2/2, sin π/3 = √3/2, and sin π/2 = 1. Of course, this table does not include the value of sin 2pi in it. We will find that sin of 2pi is 0 using various methods here. Also, we will solve some example problems using this.
| 1. | What is Sin of 2pi? |
| 2. | Sin of 2pi Using Double Angle Formula |
| 3. | Sin of 2pi Using Reference Angles |
| 4. | Sin of 2pi Using Unit Circle |
| 5. | FAQs on Sin of 2pi |
What is Sin of 2pi?
The value of sin of 2pi is 0. i.e., sin 2π = 0. From trigonometric table, we know the trigonometric ratios of standard angles 0, π/6, π/4, π/3, and π/2. So this table doesn't give us the value of sin of 2pi. Usually, to find the value of any trigonometric ratio of a non-standard angle, we use the reference angles and the quadrant in which the angle lies in. We can do the same to find sin of 2pi also. The value of sin of 2pi can be easily found by using several other methods like
- Using double angle formula
- Using reference angle
- Using unit circle
We will prove that sin 2π = 0 in each of these methods.
Sin of 2pi Using Double Angle Formula
We can find the value of sin of 2pi using the double angle formula of sine which is sin 2x = 2 sin x cos x. Since we have to find the value of sin(2π), we have to substitute x = π in the above formula. Then we get:
sin 2π = 2 sin π cos π ... (1)
Since π is also a non-standard angle, we find the values of sin π and cos π using the sum and difference formulas. Then we get
sin π = sin (π/2 + π/2) = sin π/2 cos π/2 + cos π/2 sin π/2 = (1)(0) + (0)(1) = 0
cos π = cos (π/2 + π/2) = cos π/2 cos π/2 - sin π/2 sin π/2 = (0)(0) - (1)(1) = -1
Substitute these values in (1),
sin 2π = 2 (0) (-1) = 0
Hence, sin of 2pi = 0.
Sin of 2pi Using Reference Angles
If we convert 2π into degrees, we get 360°. Since 360° lies in the interval [0°, 360°], its coterminal angle itself is the reference angle. To find its coterminal angle, we subtract 360° from it. Then we get 360° - 360° = 0°. So the coterminal angle of 360° is 0°. Also, we know that 360° means one full rotation and thus it comes either in the first quadrant or in the fourth quadrant. Let us consider both cases.
- First Quadrant: We know that in the first quadrant, sin is positive.
Then sin 360° = + sin 0° = 0 (because sin 0° = 0) - Fourth Quadrant: We know that in the fourth quadrant, sin is negative.
Then sin 360° = - sin 0° = 0 (because sin 0° = 0)
From both the cases, sin 360° = sin 2π = 0.
Hence, sin 2π = 0.
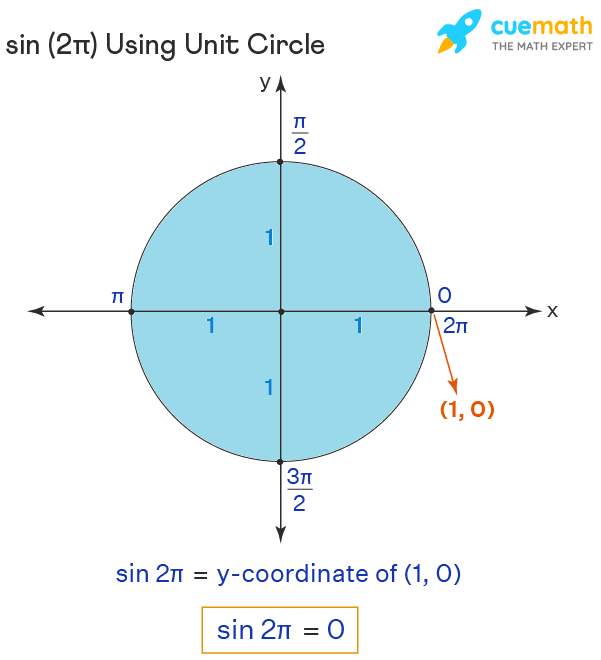
Sin of 2pi Using Unit Circle
Before finding the value of sin of 2pi using unit circle, let us recollect a few points about the unit circle.
- A unit circle is a circle of radius centered at the origin.
- Every point on the unit circle corresponds to an angle.
- This angle is made by the line joining the origin and the point with the positive direction of the x-axis in the anti-clockwise direction.
- If P(x, y) corresponds to some angle θ, then x = cos θ and y = sin θ. i.e., the y-coordinate of the point represents the sine of the corresponding angle.
As 2π (which is nothing but 360°) represents one full rotation, it is nothing but the angle made by the x-axis with itself and thus, it is equivalent to 0° on the unit circle. We also know that 0° corresponds to the point (1, 0) on the unit circle (as it is a point on the unit circle present on the x-axis). Thus,
sin 2π = sin 0° = y-coordinate of (1, 0) = 0.
Hence, sin 2π = 0.
You can visualize it from the following figure.
Important Notes:
Here are some important notes that are related to sin of 2pi.
- sin 2π = 0
- cos 2π = 1
- tan 2π = 0
- sin of any multiple of π is 0. i.e., sin nπ = 0, for any integer 'n'.
For example, sin(-2π) = 0, sin π = 0,
Related Topics:
Here are some topics are related to sin of 2pi.
FAQs on Sin of 2pi
What Is Sin of 2pi?
The value of sin of 2 pi is 0. This is because 2π is nothing but 0 degrees on the unit circle. Thus, sin 2π = sin 0 = 0.
What Is the Value of Square of Sin of 2pi?
We have sin(2π) = 0. From this, sin2(2π) = (sin 2π)2 = 02 = 0. Thus, the value of square of sin of 2pi is 0.
What is Sin^2(pi/2)?
We know that sin π/2 = 1. So sin2π/2 = (sin π/2)2 = 12 = 1.
Is Sin of 2pi Undefined?
No, sin(2π) is NOT undefined, instead sin(2π) = 0. This is because the coterminal angle of 2π is 0, from this we can conclude the value of sin of 2pi as, sin 2π = sin 0 = 0.
Why Does Sin of 2pi Equal To Zero?
Since 2π is an angle that is in the interval [0, 2π], its reference angle is nothing but its coterminal angle, which is 0. Thus, sin of 2pi can be given as, sin 2π = sin 0 = 0.
How To Prove that Sin of 2pi is 0?
On the unit circle, 2π is one complete rotation and hence 2π is equivalent to the angle 0 radians. We know that 0 radians on the unit circle correspond to the point (1, 0). Thus, sin 2π = sin 0 = y-coordinate of (1, 0) = 0. Hence, sin 2π = 0.
What is the Value of cos(-2pi)?
We know that cos (-x) = cos x. So cos (-2π) = cos 2π. On unit circle, cos 2π is same as cos 0 and hence it is 1. Thus, cos(-2pi) = 1.
How To Find the Value of Sin of 2pi Using Double Angle Formula?
We have sin 2x = 2 sin x cos x. Substitute x = π in the above formula. Then for sin of 2pi, we get: sin 2π = 2 sin π cos π ... (1).
Now,
- sin π = sin (π/2 + π/2) = sin π/2 cos π/2 + cos π/2 sin π/2 = (1)(0) + (0)(1) = 0
- cos π = cos (π/2 + π/2) = cos π/2 cos π/2 - sin π/2 sin π/2 = (0)(0) - (1)(1) = -1
Substitute these values in (1),
sin 2π = 2 (0) (-1) = 0
Hence, sin 2π = 0.
What Is Tan of 2pi Using Sin of 2pi?
We know that sin of 2pi is equal to zero, i.e., sin(2π) = 0. Also we know that tan x = (sin x) / (cos x) for any x. Thus, tan(2π) = [sin(2π)] / [cos(2π)] = (0) / [cos(2π)] = 0. Hence, tan(2π) = 0.
What is the Value of Sin 2pi/3?
Let us convert 2π/3 into degrees. Then we get 2π/3 = 120°. Using unit circle, sin 120° = √3/2. Thus, sin 2pi/3 = √3/2.