Sec 60 Degrees

The value of Sec 60 degrees is 2. Sec 60 degrees in radians is written as sec (60° × π/180°), i.e., sec (π/3) or sec (1.047197. . .). In this article, we will discuss the methods to find the value of sec 60 degrees with examples.

• Sec 60°: 2
• Sec (-60 degrees): 2
• Sec 60° in radians: sec (π/3) or sec (1.0471975 . . .)

What is the Value of Sec 60 Degrees?

The value of sec 60 degrees is 2. Sec 60 degrees can also be expressed using the equivalent of the given angle (60 degrees) in radians (1.04719 . . .)

We know, using degree to radian conversion, θ in radians = θ in degrees × (pi/180°)
⇒ 60 degrees = 60° × (π/180°) rad = π/3 or 1.0471 . . .
∴ sec 60° = sec(1.0471) = 2

Explanation:

For sec 60 degrees, the angle 60° lies between 0° and 90° (First Quadrant). Since secant function is positive in the first quadrant, thus sec 60° value = 2
Since the secant function is a periodic function, we can represent sec 60° as, sec 60 degrees = sec(60° + n × 360°), n ∈ Z.
⇒ sec 60° = sec 420° = sec 780°, and so on.
Note: Since, secant is an even function, the value of sec(-60°) = sec(60°).

Methods to Find Value of Sec 60 Degrees

The secant function is positive in the 1st quadrant. The value of sec 60° is given as 2. We can find the value of sec 60 degrees by:

• Using Unit Circle
• Using Trigonometric Functions

Sec 60 Degrees Using Unit Circle

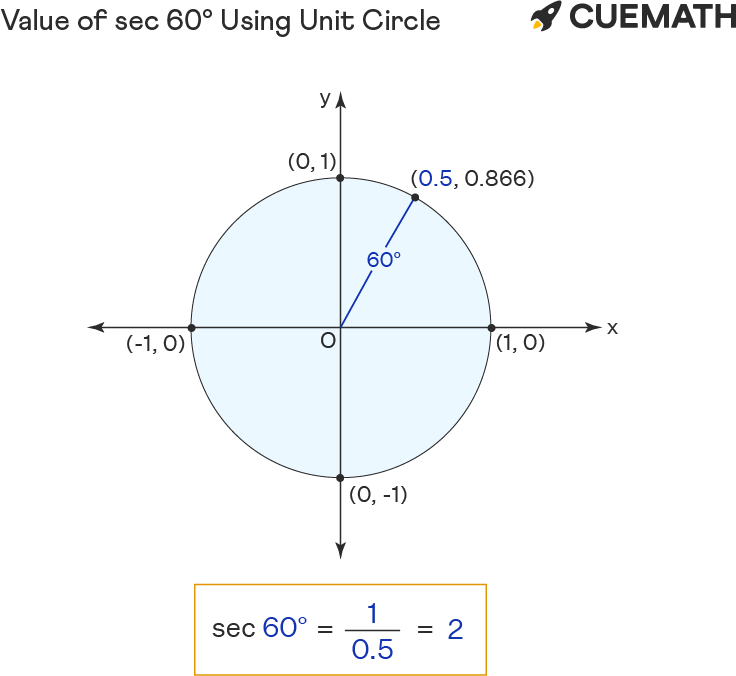
To find the value of sec 60 degrees using the unit circle:

• Rotate ‘r’ anticlockwise to form 60° angle with the positive x-axis.
• The sec of 60 degrees equals the reciprocal of the x-coordinate(0.5) of the point of intersection (0.5, 0.866) of unit circle and r.

Hence the value of sec 60° = 1/x = 2

Sec 60° in Terms of Trigonometric Functions

Using trigonometry formulas, we can represent the sec 60 degrees as:

• ± 1/√(1 - sin²(60°))
• ± √(1 + tan²(60°))
• ± √(1 + cot²(60°))/cot 60°
• ± cosec 60°/√(cosec²(60°) - 1)
• 1/cos 60°

Note: Since 60° lies in the 1st Quadrant, the final value of sec 60° will be positive.

We can use trigonometric identities to represent sec 60° as,

• -sec(180° - 60°) = -sec 120°
• -sec(180° + 60°) = -sec 240°
• cosec(90° + 60°) = cosec 150°
• cosec(90° - 60°) = cosec 30°

☛ Also Check:

• sec 330 degrees
• sec 180 degrees
• sec 90 degrees
• sec 70 degrees
• sec 120 degrees
• sec 47 degrees

FAQs on Sec 60 Degrees

What is Sec 60 Degrees?

Sec 60 degrees is the value of secant trigonometric function for an angle equal to 60 degrees. The value of sec 60° is 2.

How to Find Sec 60° in Terms of Other Trigonometric Functions?

Using trigonometry formula, the value of sec 60° can be given in terms of other trigonometric functions as:

• ± 1/√(1-sin²(60°))
• ± √(1 + tan²(60°))
• ± √(1 + cot²(60°))/cot 60°
• ± cosec 60°/√(cosec²(60°) - 1)
• 1/cos 60°

☛ Also check: trigonometric table

What is the Value of Sec 60 Degrees in Terms of Cot 60°?

We can represent the secant function in terms of the cotangent function using trig identities, sec 60° can be written as √(1 + cot²(60°))/cot 60°. Here, the value of cot 60° is equal to 0.57735.

What is the Exact Value of Sec 60 Degrees?

The exact value of sec 60 degrees is 2.

How to Find the Value of Sec 60 Degrees?

The value of sec 60 degrees can be calculated by constructing an angle of 60° with the x-axis, and then finding the coordinates of the corresponding point (0.5, 0.866) on the unit circle. The value of sec 60° is equal to the reciprocal of the x-coordinate(0.5). ∴ sec 60° = 2.