Reciprocal of Sine
The reciprocal of sine is the cosecant function. There are six main trigonometric functions namely, sine, cosine, tangent, cotangent, secant, and cosecant. An important thing to note is that the reciprocal of sine is not the inverse function of sine, that is, the cosecant function is not the inverse function of sine. So, we have cosecant which is the reciprocal of sine.
In this article, let us learn about the properties of the reciprocal of sine, that is, cosecant, its formula, domain, range, derivative, integral and graph.
What is Reciprocal of Sine?
The reciprocal of the sine function is a trigonometric function, called the cosecant function. The reciprocal of the cosecant function is the sine function itself. The product of the reciprocal of sine and the sine function is always equal to 1. Reciprocal of sine is written as cosec x = 1/sin x. The reciprocal of sine, that is cosecant function is the ratio of the hypotenuse to the perpendicular in a right-angled triangle.
Reciprocal of Sine Formula
Since sine function is the ratio of the lengths of the opposite side to the angle in consideration and hypotenuse in a right-angled triangle, the reciprocal of sine is the ratio of the hypotenuse and the opposite side of a right-angled triangle. In other words, the reciprocal of sine is the ratio of the hypotenuse to the perpendicular in a right-angled triangle. The formula of reciprocal of sine is:
Reciprocal of sine = cosecant function
= cosec x
= 1/sin x
= Hypotenuse/Perpendicular
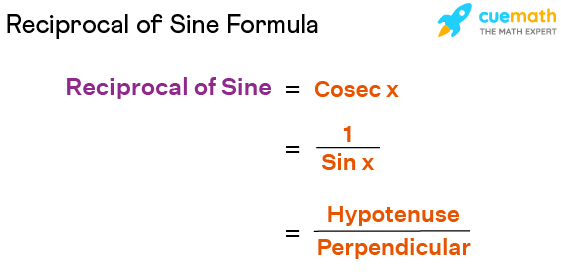
Domain and Range of Reciprocal of Sine
Since reciprocal of sine is the cosecant function, and its formula is 1/sin x, it is defined at all values of x except the values where sin x is zero as 1/sin x becomes undefined where sin x = 0. Now, we know that sin x is zero at all integral multiples of π, that is, nπ, where n is an integer. Therefore, the domain of reciprocal of sine is all real numbers except nπ, where n is an integer. The range of the reciprocal of sine is (-∞ , -1] U [1, + ∞).
Graph of Reciprocal of Sine
The graph of reciprocal of sine, that is, cosecant is a discontinuous graph. The cycle length of the reciprocal of sine function (the period after which it starts repeating) is 2π. Thus, for every value of x in the domain, we can say that cosec(x+2π) = cosec x.
- When θ = 0°, sin θ = 0 and csc 0 = not defined, we cannot evaluate csc θ.
- When θ = 90°, sin θ = 1, csc θ = 1
- When θ = -90°, sin θ = - 1, csc θ = -1
- When θ = ± 180°, sin θ = 0, csc 0 = not defined
- When θ = 270°, sin θ = -1, csc θ = - 1
- If θ is very small and positive, sinθ is positive and hence, csc θ is large and positive.
- We get vertical asymptotes when csc θ cannot be evaluated, that is at sin 0 and at θ = nπ, n is an integer

Derivative and Integral of Reciprocal of Sine
We know that the derivative of sin x is cos x. So, derivative of reciprocal of sine is given by d(1/sin x)/dx = -(1/sin2x)cos x = -(cos x/sin x)(1/sin x) = -cot x cosec x. Hence, the derivative of reciprocal of sine, that is, cosecant function is given by d(cosec x)/dx = -cot x cosec x. Similarly, we can evaluate the integral of reciprocal of sine, that is, cosec x which is given by ∫cosec x = ln|cosec x - cot x| + C.
Properties of Reciprocal of Sine
Now, that we have studied many facts and formulas of the reciprocal of sine, let us go through some of the important properties of the reciprocal of sine:
- The cosecant function is the reciprocal of the sine function.
- When sin x approaches zero, cosec x approaches infinity.
- The reciprocal of the sine graph has a period of 2π.
- cosec 0 is not defined and at all nπ, the cosecant graph has vertical asymptotes.
- The reciprocal of the sine function is symmetrical about the x-axis. It is an odd function, that is, cosec(−θ) = −cosec θ
Important Notes on Reciprocal of Sine
-
When sine reaches its maximum value of 1, the reciprocal of sine will reach its value of 1
-
When sine reaches its minimum value of –1, the reciprocal of sine will reach its value of –1
-
When sine is positive < 1, the reciprocal of sine will be positive >1
-
When sine is negative but > –1, the reciprocal of sine will be negative but < –1.
Topics Related to Reciprocal of Sine
Reciprocal of Sine Examples
-
Example 1: Determine the value of the reciprocal of sine when sin x = √3/2
Solution: We know that the reciprocal of the sine formula is 1/sin x.
Therefore, reciprocal of sine = 1/sin x
= 1/(√3/2)
= 2/√3
Answer: Reciprocal of sine is 2/√3 when sin x = √3/2
-
Example 2: Find the value of reciprocal of sine when the hypotenuse and perpendicular of a right-angled triangle are 5 and 4 units respectively.
Solution: Reciprocal of sine formula is Hypotenuse/Perpendicular, we have
Reciprocal of sine = Hypotenuse/Perpendicular
= 5/4
Answer: Reciprocal of sine = 5/4

FAQs on Reciprocal of Sine
What is Reciprocal of Sine in Trigonometry?
The reciprocal of the sine function is a trigonometric function, called the cosecant function.
What is the Reciprocal of Sine Formula?
The reciprocal of sine is the ratio of the hypotenuse and the opposite side of a right-angled triangle. The formula of reciprocal of sine is:
Reciprocal of sine = cosecant function
= cosec x
= 1/sin x
= Hypotenuse/Perpendicular
Why is Cosecant the Reciprocal of Sine?
Since sine function is the ratio of the lengths of the opposite side to the angle in consideration and hypotenuse in a right-angled triangle, the reciprocal of sine is the ratio of the hypotenuse and the opposite side of a right-angled triangle which is the formula for the cosecant function. Hence, cosecant is the reciprocal of sine.
How to Find the Reciprocal of Sine?
The reciprocal of sine can be calculated by using the formula 1/sin x = Hypotenuse/Perpendicular.
Is Cosecant the Reciprocal of Sine?
Yes, cosecant is the reciprocal of the sine function as cosec x = 1/sin x = Hypotenuse/Opposite Side
What is Reciprocal of Sine Ratio?
The reciprocal of sine ratio is equal to the ratio of the hypotenuse and perpendicular of the right-angled triangle, that is, Hypotenuse/Perpendicular.
visual curriculum
