Tan2x Formula
Tan2x is an important trigonometric function. Tan2x formula is one of the very commonly used double angle trigonometric formulas and can be expressed in terms of different trigonometric functions such as tan x, cos x, and sin x. As we know that tan x is the ratio of sine and cosine function, therefore the tan2x identity can also be expressed as the ratio of sin 2x and cos 2x.
In this article, we will learn the tan2x and tan^2x formula, its proof, and express it in terms of different trigonometric functions. We will also explore the graph of tan2x and its period along with the concept of tan square x and solve examples for a better understanding.
| 1. | What is Tan2x in Trigonometry? |
| 2. | Tan2x Formula |
| 3. | Tan2x Formula Proof |
| 4. | Tan2x Graph |
| 5. | Tan^2x (Tan Square x) |
| 6. | Tan^2x Formula |
| 7. | Tan2x Formula in Terms of Cos |
| 8. | FAQs on Tan2x Formula |
What is Tan2x in Trigonometry?
Tan2x is a trigonometric function and has a formula that is used to solve various problems in trigonometry. Tan2x is an important double angle formula, that is, a trigonometry formula where the angle is doubled. It can be expressed in terms of tan x and also as a ratio of sin2x and cos2x. Since the reciprocal of tan x is cot x, therefore we can write tan2x as the reciprocal of cot 2x, that is, tan2x = 1/cot2x. Let us see the tan2x formula:
Tan2x Formula
We can express the tan2x formula in two different forms. It can be expressed in terms of tangent function only and as a combination of the sine function and cosine function. The formula for tan2x identity is given as:
- tan2x = 2tan x / (1−tan2x)
- tan2x = sin 2x/cos 2x
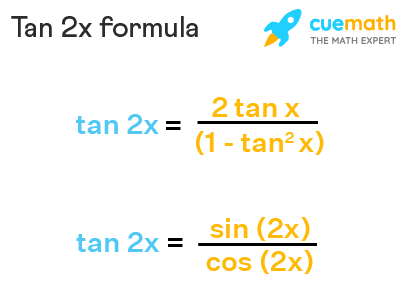
Tan2x Formula Proof
Tan2x formula can be derived using two different methods. First, we will use the angle addition formula for the tangent function to derive the tan2x identity. Note that we can write the double angle 2x as 2x = x + x. We will use the following trigonometric formula to prove the formula for tan2x:
We have
tan2x = tan (x + x)
= (tan x + tan x)/(1 - tan x tan x)
= 2 tan x/(1 - tan2x)
Hence, we have derived the tan2x formula using the angle sum formula of the tangent function.
Tan2x Identity Proof Using Sin and Cos
Now, we will derive the tan2x formula by expressing tan as a ratio of sin and cos. We will use the following trigonometric formulas:
- tan x = sin x/ cos x
- sin 2x = 2 sin x cos x
- cos 2x = cos2x - sin2x
Using the above formulas, we have
tan2x = sin 2x/cos 2x
= 2 sin x cos x/(cos2x - sin2x)
Divide the numerator and denominator of 2 sin x cos x/(1 - 2 sin2x) by cos2x
tan2x = [2 sin x cos x/cos2x]/[(cos2x - sin2x)/cos2x]
= (2 sin x/cos x)/(1 - sin2x/cos2x)
= 2 tan x/(1 - tan2x)
Hence we have derived the tan2x formula by expressing it as a ratio of sin 2x and cos 2x.
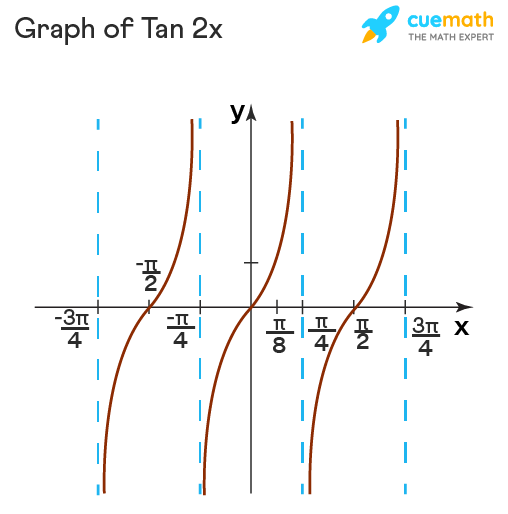
Tan2x Graph
The graph of tan2x looks similar to the graph of tan x. We know that the period of tan x is π. Since the period of tan bx is given by π/|b|, the period of tan2x is π/2. Given below is the graph of tan2x and as we can observe from the graph, the value of tan2x repeats after every π/2 radians. Also, the value of tanx is equal to zero whenever x is an integral multiple of π, therefore tan2x is equal to zero whenever 2x = nπ, where n is an integer which implies the below graph has x-intercepts at x = nπ/2.
Tan^2x (Tan Square x)
Tan^2x is the square of the trigonometric function tanx. We can derive the tan square x formulas using the trigonometric identities and formulas which consist of tan^2x. As we know that tan x can be expressed as the ratio of sinx and cosx, therefore we can express tan^2x can as the ratio of sin square x and cos square x. We use the tan^2x formula to solve complex integration and differentiation problems and simplify trigonometric expressions. In the next section, we will derive and discuss the formula of tan square x.
Tan^2x Formula
Now, we have a trigonometric identity 1 + tan^2x = sec^2x which implies tan^2x = sec^2x - 1. Since tan x can be expressed as the ratio of sine function and cosine function, therefore we can write tans square x as the ratio of sin square x and cos square x, therefore we have tan^2x = sin^2x / cos^2x. Also, we know that tan x is the reciprocal of cot x, therefore we can write tan^2x = 1/cot^2x. Hence, the list of tan^2x formula is:
- tan^2x = sec^2x - 1 ⇒ tan2x = sec2x - 1
- tan^2x = sin^2x / cos^2x ⇒ tan2x = sin2x/cos2x
- tan^2x = 1/cot^2x ⇒ tan2x = 1/cot2x
Tan2x in Terms of Cos
We can derive the tan2x formula in terms of cos. We will use the following trigonometric formulas to express tan2x in terms of cos x.
- tan x = sin x/ cos x
- sin 2x = 2 sin x cos x
- cos 2x = 2 cos2x - 1
- sin x = √(1 - cos2x)
Using the above formulas, we have
tan2x = sin 2x/ cos 2x
= 2 sin x cos x/(2 cos2x - 1)
= [2 √(1 - cos2x) cos x/(2 cos2x - 1)]
Similarly, we can write tan2x in terms of sin using the trigonometric identities.
tan2x = [2 sin x/(1 - 2 sin2x)]√(1 - sin2x)
Important Notes on Tan 2x Formula
- tan2x = 2tan x / (1 − tan2x)
- tan2x = sin 2x/cos 2x
- The derivative of tan2x is 2 sec2(2x)
- The integral of tan2x is (-1/2) ln |cos 2x| + C or (1/2) ln |sec 2x| + C.
☛ Related Articles:
Tan2x Examples
-
Example 1: Determine the value of tan2x if tan x = 4/3.
Solution: We know that tan2x = 2tan x / (1 − tan2x). If tan x = 4/3, we have tan2x = 16/9.
tan2x = 2tan x / (1 − tan2x)
= 2(4/3)/(1 - 16/9)
= (8/3)/(-7/9)
= -24/7
Answer: tan2x = -24/7
-
Example 2: Find the value of tan2x if sin x = 12/13 and cos x = 5/13
Solution: We know that tan2x = sin 2x/ cos 2x
= 2 sin x cos x /(cos2x - sin2x)
= [2 × (12/13) × (5/13)] / [(25/169) - (144/169)]
= (120/169) / (-119/169)
= -120/119
Answer: tan2x = -120/119
-
Example 3: Evaluate the derivative and integral of tan2x.
Solution: We know that the derivative of trigonometric function tan x is given by sec2x. The derivative of tan2x can be calculated using different methods such as the chain rule and quotient rule. Let us determine the derivative of tan2x using the chain rule.
d(tan2x)/dx = d(tan 2x)/d(2x) × d(2x)/dx
= sec22x × 2
= 2 sec2(2x)
Now, we will determine the integral of tan2x. We know that the integral of tan x is -ln |cos x| + C or ln |sec x| + C. Using the formulas of integration, the integral of tan2x is given by,
∫ tan2x = (-1/2) ln |cos 2x| + C
= (1/2) ln |sec 2x| + C
Answer: Hence the derivative of tan2x is 2 sec2(2x) and the integral of tan2x is given by (-1/2) ln |cos 2x| + C or (1/2) ln |sec 2x| + C.

FAQs on Tan2x Formula
What is Tan2x in Trigonometry?
Tan2x formula is one of the very commonly used double angle trigonometric formulas and can be expressed in terms of different trigonometric functions such as tan x, cos x, and sin x. The commonly used formula for tan2x is tan2x = 2tan x / (1 − tan2x).
What is Tan2x Formula?
Tan2x formula can be expressed in different ways such as:
- tan2x = 2tan x / (1 − tan2x)
- tan2x = sin 2x/cos 2x
- tan2x = [2 cos x/(2 cos2x - 1)]√(1 - cos2x)
- tan2x = [2 sin x/(1 - 2 sin2x)]√(1 - sin2x)
What is the Domain and Range of Tan2x?
The domain of tan2x consists of all real numbers except those where tan2x is not defined. So, the domain of tan 2x is R - {(2n + 1)π/4, n ∈ Z}. The range of tan2x is all real numbers, that is, R.
How to Find the Derivative of Tan2x?
The derivative of tan2x can be calculated using different methods such as the chain rule and quotient rule. The derivative of tan2x is 2 sec2(2x).
What is the Integral of Tan2x?
The integral of tan2x is given by (-1/2) ln |cos 2x| + C or (1/2) ln |sec 2x| + C.
What is the Formula of Tan2x in Terms of Cos x and Sin x?
Tan2x formula in terms of sin x and cos x is given by tan2x = 2 sin x cos x /(cos2x - sin2x)
What is Tan Square x?
Tan square x is the square of the trigonometric function tan x and is mathematically written as tan^2x. We use the tan^2x formula to solve complex integration and differentiation problems and simplify trigonometric expressions.
What is Tan^2x Formula?
The formula for tan^2x are:
- tan^2x = sec^2x - 1 ⇒ tan2x = sec2x - 1
- tan^2x = sin^2x / cos^2x ⇒ tan2x = sin2x/cos2x
- tan^2x = 1/cot^2x ⇒ tan2x = 1/cot2x
What is the Difference Between tan2x and tan^2x?
Tan2x is a double angle trigonometric formula which gives the value of the tangent function for the compound angle 2x. On the other hand, tan^2x is the whole square of the trigonometric function tanx. The value of tan2x can be both positive and negative whereas the value of tan^2x is always non-negative as the square of a number is never negative.
visual curriculum