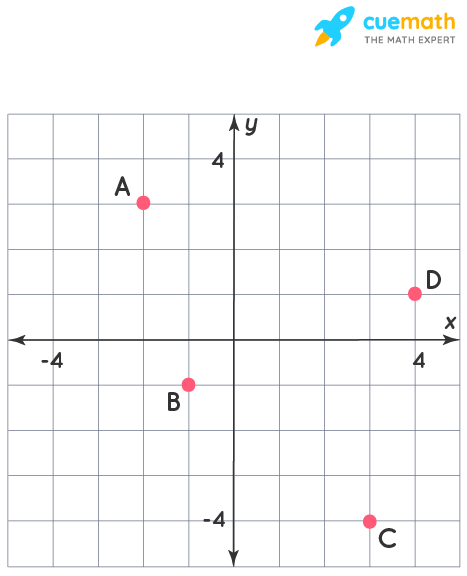
Write all of the complex numbers that are graphed in the complex plane shown. A: _ + _i, B: _ + _i, C: _ + _i, D: _ + _i
Solution:
A complex number is the sum of a real number and an imaginary number and it is represented as x + iy, where x, y are real numbers. A complex number is usually denoted by z.
A complex number is represented as z = x + iy. Here, both x and y are real numbers.
- x is called the real part which is denoted by Re(z).
- y is called the imaginary part which is denoted by Im(z).
- i is an imaginary number.
Based on the definition we will look into the x and y coordinates of each of the points A, B, C, and D showed in the graph.

Let's look into the coordinates (x,y) of each of these points along with their representation in complex form.
| Coordinates of the Points (x,y) | Complex Number Representation = x + iy |
| A(-2, 3) | -2 + 3i |
| B(-1, -1) | -1 - 1i |
| C(3, -4) | 3 - 4i |
| D(4, 1) | 4 + 1i |
We can use Cuemath's Online complex numbers calculator to perform different arithmetic operations on complex numbers.
Thus, we have represented the given points A: -2 + 3i, B: -1 - 1i, C: 3 - 4i, D: 4 + 1i in their complex form.
Write all of the complex numbers that are graphed in the complex plane shown. A: _ + _i, B: _ + _i, C: _ + _i, D: _ + _i
Summary:
The complex numbers that are graphed in the complex plane shown are, A: -2 + 3i, B: -1 - 1i, C: 3 - 4i, D: 4 + 1i
visual curriculum
