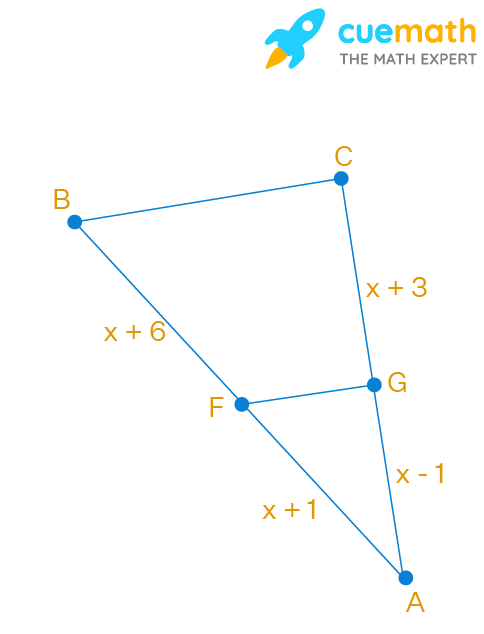
Which value of x would make △AFG similar to △ABC?

Solution:

From the given figure we can see that FG is parallel to BC (FG ∥ BC)

Also we can assume that △AFG is similar to △ABC by either SAS of SSS rule.

Therefore,

AG/AC = AF/AB

AG/(AG + GC) = AF/(AF + FB)

(x - 1)/(x - 1 + x + 3) = (x + 1)/(x + 1 + x + 6)

(x - 1)/(2x + 2) = (x + 1)/(2x + 7)

(x - 1)/2(x + 1) = (x + 1)/(2x + 7)

(x - 1)(2x + 7) = 2(x + 1)(x + 1)

2x² - 7 - 2x + 7x = 2(x² + 2x + 1)

2x² + 5x - 7 = 2x² + 4x + 2

5x - 4x = 7 + 2

x = 9

Hence the value of x = 9 will make the △AFG similar to △ABC.

---

Which value of x would make △AFG similar to △ABC?

Summary:

The value of x which will make △AFG similar to △ABC is 9.