What is the slope for the line perpendicular to the line shown in the graph?
-3, -1/3, 3, 1/3

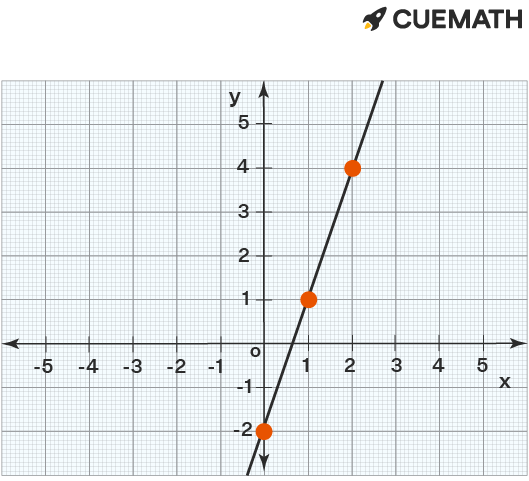
Solution:

Given line passes through the points (0, -2), (1,1), (2, 4)

Slope of the line shown in the graph can be found by using the formula

m = (y\(_2\) - y\(_1\))/(x\(_2\) - x\(_1\))

Slope of the line joining (0, -2), (2, 4) {by considering any two points on the line}

Slope of the line = (4 - (-2))/(2 - 0)

= 6/2

= 3

We have the condition that if m is the slope of the line then the slope of the perpendicular line is -1/m.

Therefore, the slope of the perpendicular line is -1/3.

The perpendicular line to the given line is shown below.

What is the slope for the line perpendicular to the line shown in the graph?

Summary:

The slope for the line perpendicular to the line shown in the graph is -1/3. Perpendicular lines are lines that meet at right angles.