What is the perimeter of a rhombus whose diagonals are 16 cm and 30 cm?

Solution:

Perimeter of a Rhombus with Diagonals

Let us learn how to find the perimeter of rhombus when diagonals are given. A rhombus is a quadrilateral with four equal sides. The perimeter of a rhombus with diagonals can be calculated using the formula of perimeter of rhombus with diagonals.

The given rhombus has diagonals of length 16 cm and 30 cm. We know that the diagonals of a rhombus bisect each other into equal parts. Observe the rhombus given below which shows that the diagonals of 16 cm and 30 cm bisect each other and, therefore, AO = 15 cm and OB = 8 cm.

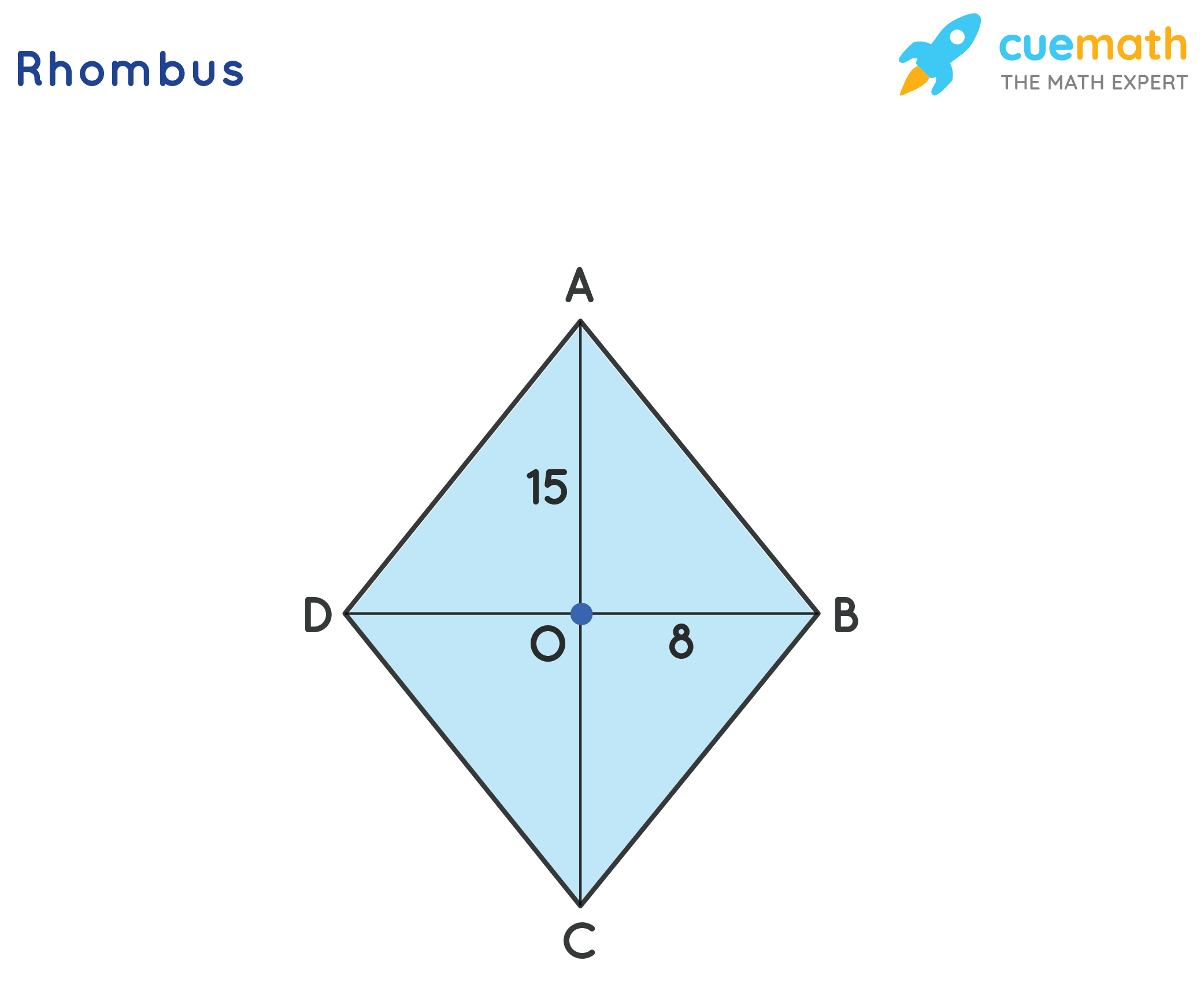
In other words, AC = 30 cm and BD = 16 cm

Therefore, AO = 15 cm and OB = 8 cm

Now to find the perimeter, we need the length of AB.

Let us find AB using the pythagoras theorem in △AOB,

AB² = AO² + OB²

AB² = 15² + 8²

AB² = 225 + 64

AB² = 289

AB = √289

AB = 17 cm

Therefore, the length of one side of the rhombus is AB = 17 cm.

The Perimeter of the rhombus: P = 4 × length of the side

P = 4 × 17 cm

P = 68 cm

Therefore, the perimeter of a rhombus whose diagonals are 16 and 30 is 68 cm.

What is the perimeter of a rhombus whose diagonals are 16 cm and 30 cm?

Summary:

The perimeter of a rhombus whose diagonals are 16 cm and 30 cm is 68 cm.