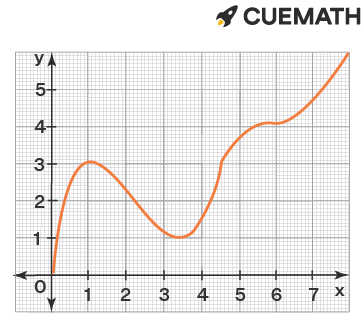
Use the given graph f over the interval (0, 7) to find the following:
(a) The open intervals on which f is increasing.
(b) The open intervals on which f is concave upward.
(c) The open intervals on which f is concave downward.
(d) The coordinates of the points of inflection.

Solution:

Given, graph f over the interval (0, 7)

a) The open intervals on which f is increasing

f is increasing when the graph slopes upwards. We observe that the graph slopes upwards when x is between 0 and 1, when x is between 3 and 7.

In interval notation, we obtain (0, 1) ∪ (3, 7)

b) The open intervals on which f is concave upward.

f is concave upward when the function decreases less and less, or the function increases more and more, i.e. the slope of the function increases.

This occurs when x is between 2 and 4 and when x is between 5 and 7.

In interval notation, we obtain (2, 4) ∪ (5, 7)

c) The open intervals on which f is concave downward.

f is concave downward when the function increases less and less, or the function decreases more and more, i.e. the slope of the function decreases.

This occurs when x is between 0 and 2 and when x is between 4 and 5.

In interval notation, we obtain (0, 2) ∪ (4, 5)

d) The coordinates of the points of inflection

The inflection points are the points where the function changes from concave upward to concave downward or from concave downward to concave upward.

From (b) and (c), we observe the inflection points are at x = 2, x = 4 and x = 5.

To determine the corresponding y-values from the given graph which results in the following coordinates of the points of inflection.

(x, y) = (2, 2)

(x, y) = (4.5, 3)

(x, y) = (5, 4)

Therefore,

(a) The open intervals on which f is increasing is (0, 1) ∪ (3, 7).

(b) The open intervals on which f is concave upward is (2, 4) ∪ (5, 7).

(d) The coordinates of the points of inflection

(x, y) = (2, 2)

(x, y) = (4.5, 3)

(x, y) = (5, 4).