Identify the vertex and the axis of symmetry of the graph of the function y = 2(x+2)2 - 4
Solution:
It is given that,
y = 2(x + 2)2 - 4
We know that the equation of a vertical parabola into vertex form is equal to,
y = a(x - h)2 + k
where, (h, k) is the vertex of the parabola,
So, the axis of symmetry of a vertical parabola is equal to
x = h … [the x coordinate of the vertex]
Then,
y = 2(x + 2)2 - 4
The vertex point (-2, -4)
Hence the axis of symmetry is equal to the coordinate of the vertex,
x = -2
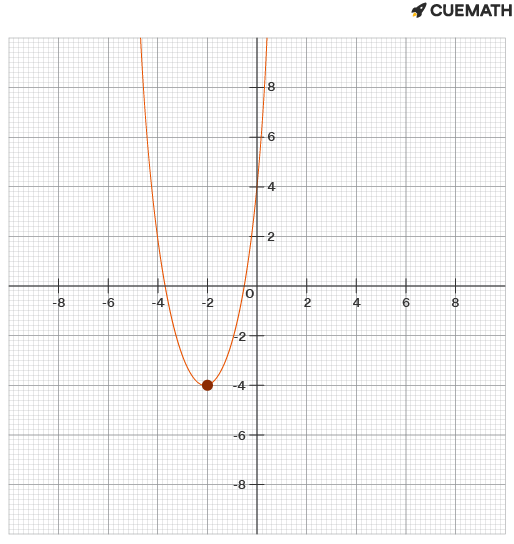
Therefore, the vertex and the axis of symmetry of the graph of the function y = 2(x+2)2 - 4 are (-2, -4) and x= -2 respectively.
Identify the vertex and the axis of symmetry of the graph of the function y = 2(x+2)2 - 4
Summary:
The vertex and the axis of symmetry of the graph of the function y = 2(x+2)2 - 4 are (-2, -4) and x= -2 respectively.