A day full of math games & activities. Find one near you.

A∩B Formula

A intersection B is a set that contains elements that are common in both sets A and B. The symbol used to denote the intersection of sets A and B is ∩, it is written as A∩B and read as 'A intersection B'. The intersection of two or more sets is the set of elements that are common to every set. A∩B can be determined easily by checking the elements that are present in both A and B. Let us go through the concept of A∩B with the help of some solved examples for a better understanding.

1.	What is A Intersection B Formula?
2.	What Is P(A∩B) Formula?
3.	Number of Elements in A∩B
4.	FAQs on A∩B Formula

What is A Intersection B Formula?

A∩B is a set that consists of elements that are common in both A and B. The formula A intersection B represents the elements that are present both in A and B and is denoted by A∩B. So, using the definition of the intersection of sets, A intersection B formula is:

A∩B = {x : x ∈ A and x ∈ B}

What Is P(A∩B) Formula?

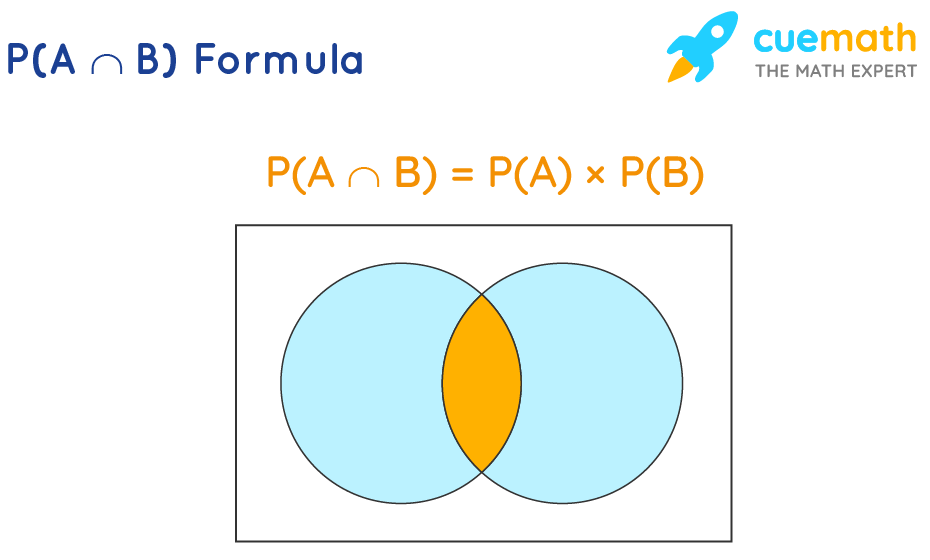
P(A∩B) is the probability of both independent events “A” and "B" happening together. The symbol "∩" means intersection. This formula is used to quickly predict the result. When events are independent, we can use the multiplication rule, which states that the two events A and B are independent if the occurrence of one event does not change the probability of the other event. P(A∩B) formula can be written as P(A∩B) = P(A) × P(B). P(A∩B) formula is given as:

P(A∩B) Formula

P(A∩B) = P(A) × P(B)

where,

P(A∩B) = Probability of both independent events “A” and "B" happening together.
P(A) = Probability of an event “A”
P(B) = Probability of an event “B”

To calculate P(A∩B) for dependent events, we use the concept of conditional probability and rewrite the formula as,

P(A∩B) = P(A|B)P(B) or P(A∩B) = P(B|A)P(A)

Number of Elements in A∩B

To determine the number of elements in A intersection B, we will use the formula for A union B. We know that the number of elements in A U B is given by n(A U B) = n(A) + n(B) - n(A ∩ B), where

n(A U B) = Number of elements in A U B
n(A) = Number of elements in A
n(B) = Number of elements in B
n(A ∩ B) = Number of elements in A ∩ B

By taking n(A ∩ B) to one side and all other terms on another side, the formula for the number of elements in A∩B is given as,

n(A∩B) = n(A) + n(B) - n(A U B)

Important Notes on A Intersection B Formula

A∩B = {x : x ∈ A and x ∈ B}
A∩B = B∩A
n(A∩B) = n(A) + n(B) - n(A U B)
For independent events A and B, P(A∩B) = P(A) × P(B)
For dependent events A and B, P(A∩B) = P(A|B)P(B) or P(A∩B) = P(B|A)P(A)

Related Topics on A∩B Formula

Examples Using A∩B Formula

Example 1: Two sets A and B are given as A = {2, 4, 6, 8, 10} and B = {1, 2, 3, 4, 5, 6}. Find A∩B.

Solution: We need to determine A intersection B, that is, elements that are common in both A and B. As we can see, the common elements are 2, 4, 6.

A∩B = {2, 4, 6}

Answer: Therefore, A∩B = {2, 4, 6}
Example 2: What is the probability of selecting a red card and a 6 when a card is randomly selected from a deck of 52 cards? Solve this by using the P(A∩B) formula.

Solution: Let A and B be the individual probabilities of getting a red card and getting a 6 respectively.

We know that the number of red cards = 26,

The number of 6 labeled cards = 4, and

The probability of getting a red card from a deck of 52 cards, P(A) = 26/52

Since the probability of getting a red card and the probability of getting a 6 are calculated individually here, therefore the total number of cards for both cases will be taken as 52.

Thus, probability of getting a 6 from a deck of 52 cards, P(B) = 4/52

Using the P(A∩B) formula,

P(A∩B) = P(A) × P(B)

P(A∩B) = 26/52 × 4/52

= (26×4)/(52×52)

= 2/52

= 1/26

Answer: The required probability = 1 / 26.
Example 3: What is the probability of getting a 2 and 3 when a die is rolled? Solve this by using the P(A∩B) formula.

Solution: To find: The probability of getting a 2 and 3 when a die is rolled.

Let A and B be the events of getting a 2 and getting a 3 when a die is rolled.

Then, P(A) = 1 / 6 and P(B) = 1 / 6.

Using the P(A∩B) formula,

P(A∩B) = P(A) × P(B)

In this case, A and B are mutually exclusive as we cannot get 2 and 3 in the same roll of a die.

Hence, P(A∩B) = 0.

Answer: The required probability = 0.

go to slide go to slide go to slide

Breakdown tough concepts through simple visuals.

Math will no longer be a tough subject, especially when you understand the concepts through visualizations.

Book a Free Trial Class

Practice Questions on A Intersection B Formula

go to slide go to slide

FAQs on A∩B Formula

What is A∩B Formula in Set Theory?

Using the definition of the intersection of sets, A intersection B formula is: A∩B = {x: x ∈ A and x ∈ B}

What Is P(A∩B) Formula?

P(A∩B) is the probability of both independent events “A” and "B" happening together, P(A∩B) formula can be written as P(A∩B) = P(A) × P(B),
where,

P(A∩B) = Probability of both independent events “A” and "B" happening together.
P(A) = Probability of an event “A”
P(B) = Probability of an event “B”

How Do you Find A ∩ B?

A ∩ B can be determined by considering only the elements that are present in both A and B. A ∩ B consists the common elements only.

What Does (A ∩ B) Represent in P(A ∩ B) Formula?

(A ∩ B) in P(A ∩ B) Formula represents the intersection of two events A and B. Symbol '∩' denotes intersection.

How To Apply P(A ∩ B) Formula?

We apply P(A ∩ B) formula to calculate the probability of two independent events A and B occurring together. It is given as, P(A∩B) = P(A) × P(B), where, P(A) is Probability of an event “A” and P(B) = Probability of an event “B”.

How Do You Find the P(A ∩ B) Formula of Two Independent Events?

We can find the probability of the intersection of two independent events as, P(A∩B) = P(A) × P(B), where, P(A) is the Probability of an event “A” and P(B) = Probability of an event “B” and P(A∩B) is Probability of both independent events “A” and "B" happening together.

Math worksheets and
visual curriculum