Real Numbers
Real number is any number that can be found in the real world. We find numbers everywhere around us. Natural numbers are used for counting objects, rational numbers are used for representing fractions, irrational numbers are used for calculating the square root of a number, integers for measuring temperature, and so on. These different types of numbers make a collection of real numbers. In this lesson, let us learn all about what are real numbers, the subsets of real numbers along with real numbers examples.
| 1. | What are Real Numbers? |
| 2. | Symbol of Real Numbers |
| 3. | Properties of Real Numbers |
| 4. | FAQs on Real Numbers |
What are Real Numbers?
Any number that we can think of, except complex numbers, is a real number. For example, 3, 0, 1.5, 3/2, √5, and so on are real numbers.
Definition of Real Numbers
Real numbers include rational numbers like positive and negative integers, fractions, and irrational numbers. Now, which numbers are not real numbers? The numbers that are neither rational nor irrational are non-real numbers, like, √-1, 2 + 3i, and -i. These numbers include the set of complex numbers, C.
Set of Real Numbers
The set of real numbers, which is denoted by R, is the union of the set of rational numbers (Q) and the set of irrational numbers ( \(\overline{Q}\)). So, we can write the set of real numbers as, R = Q ∪ \(\overline{Q}\). This indicates that real numbers include natural numbers, whole numbers, integers, rational numbers, and irrational numbers. Observe the following table to understand this better. The table shows the sets of numbers that come under real numbers.
| Number set | Is it a part of the set of real numbers? |
|---|---|
|
Natural Numbers |
✅ |
|
Whole Numbers |
✅ |
|
Integers |
✅ |
|
Rational Numbers |
✅ |
|
Irrational Numbers |
✅ |
|
Complex Numbers |
❌ |
List of Real Numbers
The list of real numbers is endless because it includes all kinds of numbers like whole, natural, integers, rational, and irrational numbers. Since it includes integers it has negative numbers too. So, there is no specific number from which the list of real numbers starts or ends. It goes to infinity towards both sides of the number line.
Types of Real Numbers
We know that real numbers include rational numbers and irrational numbers. Thus, there does not exist any real number that is neither rational nor irrational. It simply means that if we pick up any number from R, it is either rational or irrational.
Rational Numbers
Any number which can be defined in the form of a fraction p/q is called a rational number. The numerator in the fraction is represented as 'p' and the denominator as 'q', where 'q' is not equal to zero. A rational number can be a natural number, a whole number, a decimal, or an integer. For example, 1/2, -2/3, 0.5, 0.333 are rational numbers.
Irrational Numbers
Irrational numbers are the set of real numbers that cannot be expressed in the form of a fraction p/q where 'p' and 'q' are integers and the denominator 'q' is not equal to zero (q≠0.). For example, π (pi) is an irrational number. π = 3.14159265...In this case, the decimal value never ends at any point. Therefore, numbers like √2, -√7, and so on are irrational numbers.
Symbol of Real Numbers
Real numbers are represented by the symbol R. Here is a list of the symbols of the other types of numbers.
- N - Natural numbers
- W - Whole numbers
- Z - Integers
- Q - Rational numbers
- \(\overline{Q}\) - Irrational numbers
Subsets of Real Numbers
All numbers except complex numbers are real numbers. Therefore, real numbers have the following five subsets:
- Natural numbers: All positive counting numbers make the set of natural numbers, N = {1, 2, 3, ...}
- Whole numbers: The set of natural numbers along with 0 represents the set of whole numbers. W = {0, 1, 2, 3, ..}
- Integers: All positive counting numbers, negative numbers, and zero make up the set of integers. Z = {..., -3, -2, -1, 0, 1, 2, 3, ...}
- Rational numbers: Numbers that can be written in the form of a fraction p/q, where 'p' and 'q' are integers and 'q' is not equal to zero are rational numbers. Q = {-3, 0, -6, 5/6, 3.23}
- Irrational numbers: The numbers that are square roots of positive rational numbers, cube roots of rational numbers, etc., such as √2, come under the set of irrational numbers. ( \(\overline{Q}\)) = {√2, -√6}
Real Numbers Chart
Among the sets given above, the sets N, W, and Z are the subsets of Q. The following figure shows the real numbers chart that explains the relationship between all the numbers mentioned above.
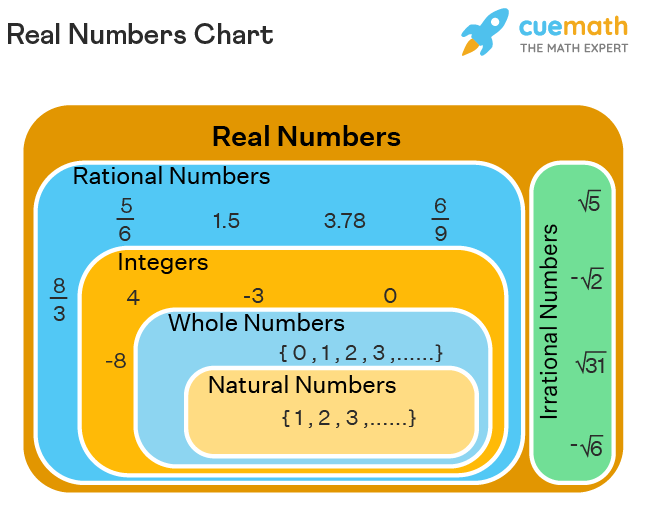
Properties of Real Numbers
- Closure Property: The closure property states that the sum and product of two real numbers is always a real number. The closure property of R is stated as follows: If a, b ∈ R, a + b ∈ R and ab ∈ R
- Associative Property: The sum or product of any three real numbers remains the same even when the grouping of numbers is changed. The associative property of R is stated as follows: If a,b,c ∈ R, a + (b + c) = (a + b) + c and a × (b × c) = (a × b) × c
- Commutative Property: The sum and the product of two real numbers remain the same even after interchanging the order of the numbers. The commutative property of R is stated as follows: If a, b ∈ R, a + b = b + a and a × b = b × a
- Distributive Property: Real numbers satisfy the distributive property. The distributive property of multiplication over addition is, a × (b + c) = (a × b) + (a × c) and the distributive property of multiplication over subtraction is a × (b - c) = (a × b) - (a × c)
Real Numbers on a Number Line
A number line helps us to display numbers by representing them by a unique point on the line. Every point on the number line shows a unique real number. Note the following steps to represent real numbers on a number line:
- Step 1: Draw a horizontal line with arrows on both ends and mark the number 0 in the middle. The number 0 is called the origin.
- Step 2: Mark an equal length on both sides of the origin and label it with a definite scale.
- Step 3: It should be noted that the positive numbers lie on the right side of the origin and the negative numbers lie on the left side of the origin.
Observe the numbers highlighted on the number line. It shows real numbers like -5/2, 0, 3/2, and 2.

Difference Between Real Numbers and Integers
The main difference between real numbers and integers is that real numbers include integers. In other words, integers come under the category of real numbers. Let us understand the difference between real numbers and integers with the help of the following table.
| Real Numbers | Integers |
|---|---|
| Real numbers include rational numbers, irrational numbers, whole numbers, and natural numbers. | Integers include negative numbers, positive numbers, and zero. |
| Examples of Real numbers: 1/2, -2/3, 0.5, √2 | Examples of Integers: -4, -3, 0, 1, 2 |
| The symbol that is used to denote real numbers is R. | The symbol that is used to denote integers is Z. |
| Every point on the number line shows a unique real number. | Only whole numbers and negative numbers on a number line denote integers. |
| Decimal and fractions are considered to be real numbers. | Integers do not include decimals and fractions. |
Important Tips on Real Numbers
- Every irrational number is a real number.
- Every rational number is a real number.
- All numbers except complex numbers are real numbers.
- All integers are real numbers.
☛ Related Articles
- Prime Numbers
- Composite Numbers
- Odd Numbers
- Irrational Numbers
- Counting Numbers
- Cardinal Numbers
- Even and Odd Numbers
- Sum of Even Numbers
- Even Numbers 1 to 100
- Even Numbers 1 to 1000
- Odd and Even Numbers Worksheets
- Rational Numbers
- Natural Numbers
- Decimal Representation of Irrational numbers
- Complex Conjugate
Cuemath is one of the world's leading math learning platforms that offers LIVE 1-to-1 online math classes for grades K-12. Our mission is to transform the way children learn math, to help them excel in school and competitive exams. Our expert tutors conduct 2 or more live classes per week, at a pace that matches the child's learning needs.
Real Numbers Examples
-
Example 1: Identify the real numbers among the following: √6, -3, 3.15, -1/2, √-5.
Solution:
Among the given numbers, √-5 is a complex number. Hence, it cannot be a real number. The other numbers are either rational or irrational. Thus, they are real numbers. Therefore, the real numbers from the list are √6, -3, 3.15, and -1/2
-
Example 2: Fill in the blanks with respect to real numbers:
a.) Real numbers are denoted by _.
b.) Positive real numbers start from _
Solution:
a.) Real numbers are denoted by the letter R.
b.) Positive real numbers start from 1 because positive numbers mean numbers that are greater than 1. Otherwise, there is no specific number from which the list of real numbers starts or ends. It goes to infinity towards both sides of the number line.
-
Example 3: State true or false with respect to real numbers.
a.) Every irrational number is a real number.
b.) Every rational number is a real number.
c.) Every real number is a complex number.
d.) Every real number is an irrational number.
e.) Every natural number is a real number.
f.) Every real number is a rational number.
Solution:
a.) True, every irrational number is a real number.
b.) True, every rational number is a real number.
c.) False, complex numbers are not real numbers.
d.) False, every real number is not an irrational number, it can be a natural number, a whole number or an integer.
e.) True, every natural number is a real number.
f.) False, every real number may not necessarily be a rational number because real numbers include irrational numbers as well.

FAQs on Real Numbers
What are Real Numbers in Math?
Real numbers include rational numbers like positive and negative integers, fractions, and irrational numbers. In other words, any number that we can think of, except complex numbers, is a real number. For example, 3, 0, 1.5, 3/2, √5, and so on are real numbers.
What are the Properties of Real Numbers?
The set of real numbers satisfies the closure property, the associative property, the commutative property, and the distributive property.
-
Closure Property: The sum and product of two real numbers is always a real number. The closure property of R is stated as follows: If a, b ∈ R, a + b ∈ R and ab ∈ R
-
Associative Property: The sum or product of any three real numbers remains the same even when the grouping of numbers is changed. The associative property of R is stated as follows: If a,b,c ∈ R, a + (b + c) = (a + b) + c and a × (b × c) = (a × b) × c
-
Commutative Property: The sum and the product of two real numbers remain the same even after interchanging the order of the numbers. The commutative property of R is stated as follows: If a, b ∈ R, a + b = b + a and a × b = b × a
- Distributive Property: The distributive property of multiplication over addition is a × (b + c) = (a × b) + (a × c) and the distributive property of multiplication over subtraction is a × (b - c) = (a × b) - (a × c)
What are the Subsets of Real Numbers?
Real numbers have the following five subsets:
- Natural numbers: N = {1, 2, 3, ...}
- Whole numbers: W = {0, 1, 2, 3, ..}
- Integers: Z = {..., -3, -2, -1, 0, 1, 2, 3, ...}
- Rational numbers: Q = {-3, 0, -6, 5/6, 3.23}
- Irrational numbers: ( \(\overline{Q}\)) = {√2, -√6}
What are Non Real Numbers?
Complex numbers, like √-1, are not real numbers. In other words, the numbers that are neither rational nor irrational, are non-real numbers.
How to Classify Real Numbers?
Real numbers can be classified into two types, rational numbers and irrational numbers. A rational number includes positive and negative integers, fractions, like, -2, 0, -4, 2/6, 4.51, whereas, irrational numbers include the square roots of rational numbers, cube roots of rational numbers, etc., such as √2, -√8
How to Represent Real Numbers on Number Line?
Real numbers can be represented on a number line by following the steps given below:
- Draw a horizontal line with arrows on both ends and mark the number 0 in the middle. The number 0 is called the origin.
- Mark an equal length on both sides of the origin and label it with a definite scale.
- Remember that the positive numbers lie on the right side of the origin and the negative numbers lie on the left side of the origin.
Is the Square Root of a Negative Number a Real Number?
No, the square root of a negative number is not a real number. For example, √-2 is not a real number. However, if the number inside the √ symbol is positive, then it will be a real number.
Is 0 a Real Number?
Yes, 0 is a real number because it belongs to the set of whole numbers and the set of whole numbers is a subset of real numbers.
Is 9 a Real Number?
Yes, 9 is a real number because it belongs to the set of natural numbers that comes under real numbers.
What is the Difference Between Real Numbers, Integers, Rational Numbers, and Irrational Numbers?
The main difference between real numbers and the other given numbers is that real numbers include rational numbers, irrational numbers, and integers. For example, 2, -3/4, 0.5, √2 are real numbers.
- Integers include only positive numbers, negative numbers, and zero. For example, -7,-6, 0, 3, 1 are integers.
- Rational numbers are those numbers that can be written in the form of a fraction p/q, where 'p' and 'q' are integers and 'q' is not equal to zero. For example, -3, 0, -6, 5/6, 3.23 are rational numbers.
- Irrational numbers are those numbers that are square roots of positive rational numbers, cube roots of rational numbers, etc., such as √2, - √5, and so on.
Where do Real Numbers Start from?
There is no specific number from where real numbers start or end because real numbers include all kinds of numbers like whole, natural, integers, rational, and irrational numbers except complex numbers. Since it includes integers it has negative numbers as well. So, the list of real numbers goes to infinity towards both sides of the number line.
visual curriculum
