A day full of math games & activities. Find one near you.

LCM of 9 and 12

LCM of 9 and 12 is the smallest number among all common multiples of 9 and 12. The first few multiples of 9 and 12 are (9, 18, 27, 36, 45, . . . ) and (12, 24, 36, 48, 60, . . . ) respectively. There are 3 commonly used methods to find LCM of 9 and 12 - by division method, by listing multiples, and by prime factorization.

1.	LCM of 9 and 12
2.	List of Methods
3.	Solved Examples
4.	FAQs

What is the LCM of 9 and 12?

Answer: LCM of 9 and 12 is 36.

Explanation:

The LCM of two non-zero integers, x(9) and y(12), is the smallest positive integer m(36) that is divisible by both x(9) and y(12) without any remainder.

Methods to Find LCM of 9 and 12

The methods to find the LCM of 9 and 12 are explained below.

By Listing Multiples
By Division Method
By Prime Factorization Method

LCM of 9 and 12 by Listing Multiples

To calculate the LCM of 9 and 12 by listing out the common multiples, we can follow the given below steps:

Step 1: List a few multiples of 9 (9, 18, 27, 36, 45, . . . ) and 12 (12, 24, 36, 48, 60, . . . . )
Step 2: The common multiples from the multiples of 9 and 12 are 36, 72, . . .
Step 3: The smallest common multiple of 9 and 12 is 36.

∴ The least common multiple of 9 and 12 = 36.

LCM of 9 and 12 by Division Method

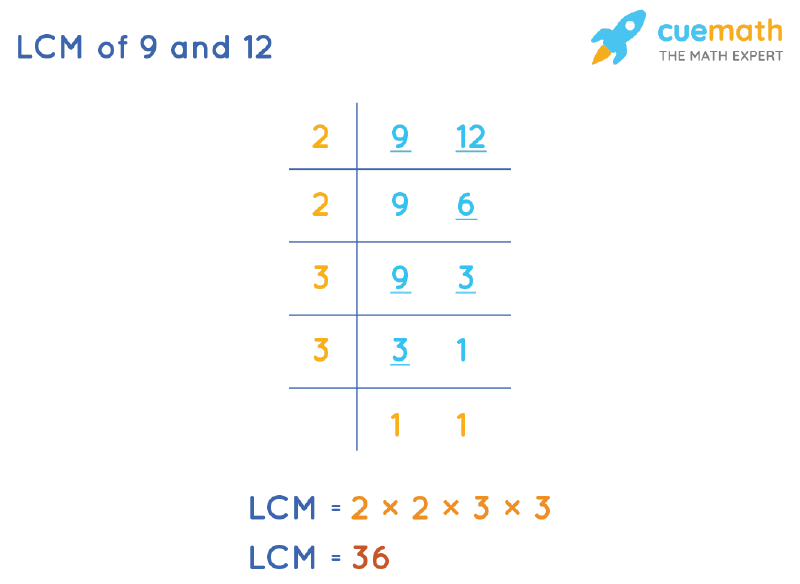
To calculate the LCM of 9 and 12 by the division method, we will divide the numbers(9, 12) by their prime factors (preferably common). The product of these divisors gives the LCM of 9 and 12.

Step 1: Find the smallest prime number that is a factor of at least one of the numbers, 9 and 12. Write this prime number(2) on the left of the given numbers(9 and 12), separated as per the ladder arrangement.
Step 2: If any of the given numbers (9, 12) is a multiple of 2, divide it by 2 and write the quotient below it. Bring down any number that is not divisible by the prime number.
Step 3: Continue the steps until only 1s are left in the last row.

The LCM of 9 and 12 is the product of all prime numbers on the left, i.e. LCM(9, 12) by division method = 2 × 2 × 3 × 3 = 36.

LCM of 9 and 12 by Prime Factorization

Prime factorization of 9 and 12 is (3 × 3) = 3² and (2 × 2 × 3) = 2² × 3¹ respectively. LCM of 9 and 12 can be obtained by multiplying prime factors raised to their respective highest power, i.e. 2² × 3² = 36.
Hence, the LCM of 9 and 12 by prime factorization is 36.

☛ Also Check:

LCM of 9 and 12 Examples

Example 1: Verify the relationship between GCF and LCM of 9 and 12.

Solution:

The relation between GCF and LCM of 9 and 12 is given as,
LCM(9, 12) × GCF(9, 12) = Product of 9, 12
Prime factorization of 9 and 12 is given as, 9 = (3 × 3) = 3² and 12 = (2 × 2 × 3) = 2² × 3¹
LCM(9, 12) = 36
GCF(9, 12) = 3
LHS = LCM(9, 12) × GCF(9, 12) = 36 × 3 = 108
RHS = Product of 9, 12 = 9 × 12 = 108
⇒ LHS = RHS = 108
Hence, verified.
Example 2: The product of two numbers is 108. If their GCD is 3, what is their LCM?

Solution:

Given: GCD = 3
product of numbers = 108
∵ LCM × GCD = product of numbers
⇒ LCM = Product/GCD = 108/3
Therefore, the LCM is 36.
The probable combination for the given case is LCM(9, 12) = 36.
Example 3: The GCD and LCM of two numbers are 3 and 36 respectively. If one number is 12, find the other number.

Solution:

Let the other number be y.
∵ GCD × LCM = 12 × y
⇒ y = (GCD × LCM)/12
⇒ y = (3 × 36)/12
⇒ y = 9
Therefore, the other number is 9.

go to slide go to slide go to slide

Ready to see the world through math’s eyes?

Math is at the core of everything we do. Enjoy solving real-world math problems in live classes and become an expert at everything.

Book a Free Trial Class

FAQs on LCM of 9 and 12

What is the LCM of 9 and 12?

The LCM of 9 and 12 is 36. To find the least common multiple of 9 and 12, we need to find the multiples of 9 and 12 (multiples of 9 = 9, 18, 27, 36; multiples of 12 = 12, 24, 36, 48) and choose the smallest multiple that is exactly divisible by 9 and 12, i.e., 36.

What is the Relation Between GCF and LCM of 9, 12?

The following equation can be used to express the relation between GCF and LCM of 9 and 12, i.e. GCF × LCM = 9 × 12.

Which of the following is the LCM of 9 and 12? 50, 15, 45, 36

The value of LCM of 9, 12 is the smallest common multiple of 9 and 12. The number satisfying the given condition is 36.

If the LCM of 12 and 9 is 36, Find its GCF.

LCM(12, 9) × GCF(12, 9) = 12 × 9
Since the LCM of 12 and 9 = 36
⇒ 36 × GCF(12, 9) = 108
Therefore, the GCF = 108/36 = 3.

What are the Methods to Find LCM of 9 and 12?

The commonly used methods to find the LCM of 9 and 12 are:

Prime Factorization Method
Division Method
Listing Multiples

Download FREE Study Materials

LCM and GCF

Math worksheets and
visual curriculum