LCM of 17 and 5
LCM of 17 and 5 is the smallest number among all common multiples of 17 and 5. The first few multiples of 17 and 5 are (17, 34, 51, 68, 85, . . . ) and (5, 10, 15, 20, . . . ) respectively. There are 3 commonly used methods to find LCM of 17 and 5 - by listing multiples, by prime factorization, and by division method.
| 1. | LCM of 17 and 5 |
| 2. | List of Methods |
| 3. | Solved Examples |
| 4. | FAQs |
What is the LCM of 17 and 5?
Answer: LCM of 17 and 5 is 85.
Explanation:
The LCM of two non-zero integers, x(17) and y(5), is the smallest positive integer m(85) that is divisible by both x(17) and y(5) without any remainder.
Methods to Find LCM of 17 and 5
Let's look at the different methods for finding the LCM of 17 and 5.
- By Prime Factorization Method
- By Division Method
- By Listing Multiples
LCM of 17 and 5 by Prime Factorization
Prime factorization of 17 and 5 is (17) = 171 and (5) = 51 respectively. LCM of 17 and 5 can be obtained by multiplying prime factors raised to their respective highest power, i.e. 51 × 171 = 85.
Hence, the LCM of 17 and 5 by prime factorization is 85.
LCM of 17 and 5 by Division Method
To calculate the LCM of 17 and 5 by the division method, we will divide the numbers(17, 5) by their prime factors (preferably common). The product of these divisors gives the LCM of 17 and 5.
- Step 1: Find the smallest prime number that is a factor of at least one of the numbers, 17 and 5. Write this prime number(5) on the left of the given numbers(17 and 5), separated as per the ladder arrangement.
- Step 2: If any of the given numbers (17, 5) is a multiple of 5, divide it by 5 and write the quotient below it. Bring down any number that is not divisible by the prime number.
- Step 3: Continue the steps until only 1s are left in the last row.
The LCM of 17 and 5 is the product of all prime numbers on the left, i.e. LCM(17, 5) by division method = 5 × 17 = 85.
LCM of 17 and 5 by Listing Multiples
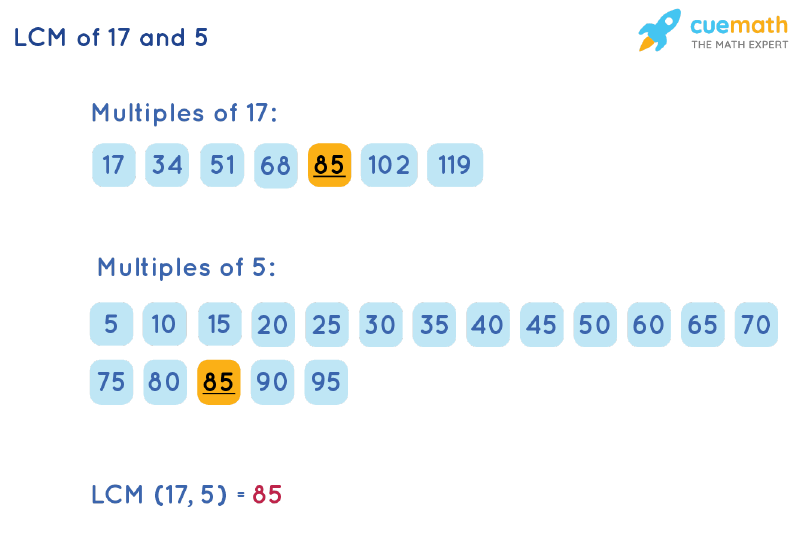
To calculate the LCM of 17 and 5 by listing out the common multiples, we can follow the given below steps:
- Step 1: List a few multiples of 17 (17, 34, 51, 68, 85, . . . ) and 5 (5, 10, 15, 20, . . . . )
- Step 2: The common multiples from the multiples of 17 and 5 are 85, 170, . . .
- Step 3: The smallest common multiple of 17 and 5 is 85.
∴ The least common multiple of 17 and 5 = 85.
☛ Also Check:
- LCM of 72 and 108 - 216
- LCM of 7, 8, 11 and 12 - 1848
- LCM of 3, 5 and 6 - 30
- LCM of 520 and 468 - 4680
- LCM of 150 and 180 - 900
- LCM of 3, 9 and 15 - 45
- LCM of 10 and 18 - 90
LCM of 17 and 5 Examples
-
Example 1: Find the smallest number that is divisible by 17 and 5 exactly.
Solution:
The value of LCM(17, 5) will be the smallest number that is exactly divisible by 17 and 5.
⇒ Multiples of 17 and 5:- Multiples of 17 = 17, 34, 51, 68, 85, 102, 119, 136, 153, 170, . . . ., 34, 51, 68, 85, . . . .
- Multiples of 5 = 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, . . . ., 70, 75, 80, 85, . . . .
Therefore, the LCM of 17 and 5 is 85.
-
Example 2: The product of two numbers is 85. If their GCD is 1, what is their LCM?
Solution:
Given: GCD = 1
product of numbers = 85
∵ LCM × GCD = product of numbers
⇒ LCM = Product/GCD = 85/1
Therefore, the LCM is 85.
The probable combination for the given case is LCM(17, 5) = 85. -
Example 3: The GCD and LCM of two numbers are 1 and 85 respectively. If one number is 5, find the other number.
Solution:
Let the other number be a.
∵ GCD × LCM = 5 × a
⇒ a = (GCD × LCM)/5
⇒ a = (1 × 85)/5
⇒ a = 17
Therefore, the other number is 17.

FAQs on LCM of 17 and 5
What is the LCM of 17 and 5?
The LCM of 17 and 5 is 85. To find the least common multiple of 17 and 5, we need to find the multiples of 17 and 5 (multiples of 17 = 17, 34, 51, 68 . . . . 85; multiples of 5 = 5, 10, 15, 20 . . . . 85) and choose the smallest multiple that is exactly divisible by 17 and 5, i.e., 85.
What are the Methods to Find LCM of 17 and 5?
The commonly used methods to find the LCM of 17 and 5 are:
- Listing Multiples
- Prime Factorization Method
- Division Method
If the LCM of 5 and 17 is 85, Find its GCF.
LCM(5, 17) × GCF(5, 17) = 5 × 17
Since the LCM of 5 and 17 = 85
⇒ 85 × GCF(5, 17) = 85
Therefore, the greatest common factor (GCF) = 85/85 = 1.
What is the Least Perfect Square Divisible by 17 and 5?
The least number divisible by 17 and 5 = LCM(17, 5)
LCM of 17 and 5 = 5 × 17 [Incomplete pair(s): 5, 17]
⇒ Least perfect square divisible by each 17 and 5 = LCM(17, 5) × 5 × 17 = 7225 [Square root of 7225 = √7225 = ±85]
Therefore, 7225 is the required number.
How to Find the LCM of 17 and 5 by Prime Factorization?
To find the LCM of 17 and 5 using prime factorization, we will find the prime factors, (17 = 17) and (5 = 5). LCM of 17 and 5 is the product of prime factors raised to their respective highest exponent among the numbers 17 and 5.
⇒ LCM of 17, 5 = 51 × 171 = 85.
visual curriculum