A day full of math games & activities. Find one near you.

HCF of 3 and 7

HCF of 3 and 7 is the largest possible number that divides 3 and 7 exactly without any remainder. The factors of 3 and 7 are 1, 3 and 1, 7 respectively. There are 3 commonly used methods to find the HCF of 3 and 7 - long division, Euclidean algorithm, and prime factorization.

1.	HCF of 3 and 7
2.	List of Methods
3.	Solved Examples
4.	FAQs

What is HCF of 3 and 7?

Answer: HCF of 3 and 7 is 1.

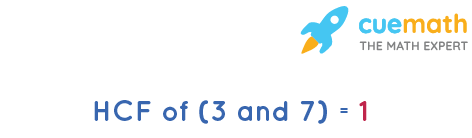
Explanation:

The HCF of two non-zero integers, x(3) and y(7), is the highest positive integer m(1) that divides both x(3) and y(7) without any remainder.

Methods to Find HCF of 3 and 7

The methods to find the HCF of 3 and 7 are explained below.

Long Division Method
Using Euclid's Algorithm
Prime Factorization Method

HCF of 3 and 7 by Long Division

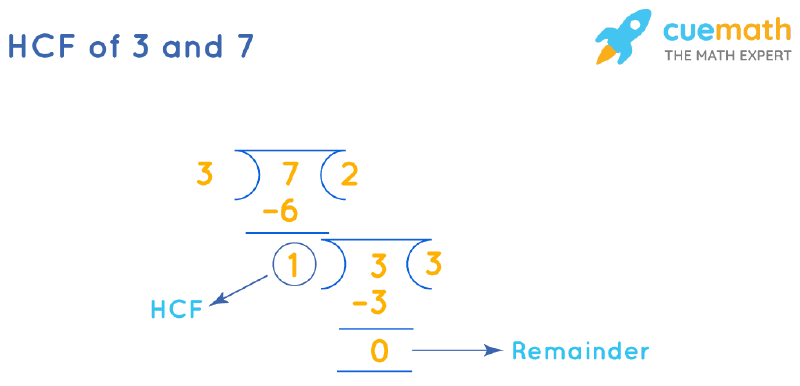
HCF of 3 and 7 is the divisor that we get when the remainder becomes 0 after doing long division repeatedly.

Step 1: Divide 7 (larger number) by 3 (smaller number).
Step 2: Since the remainder ≠ 0, we will divide the divisor of step 1 (3) by the remainder (1).
Step 3: Repeat this process until the remainder = 0.

The corresponding divisor (1) is the HCF of 3 and 7.

HCF of 3 and 7 by Euclidean Algorithm

As per the Euclidean Algorithm, HCF(X, Y) = HCF(Y, X mod Y)
where X > Y and mod is the modulo operator.

Here X = 7 and Y = 3

HCF(7, 3) = HCF(3, 7 mod 3) = HCF(3, 1)
HCF(3, 1) = HCF(1, 3 mod 1) = HCF(1, 0)
HCF(1, 0) = 1 (∵ HCF(X, 0) = |X|, where X ≠ 0)

Therefore, the value of HCF of 3 and 7 is 1.

HCF of 3 and 7 by Prime Factorization

Prime factorization of 3 and 7 is (3) and (7) respectively. As visible, there are no common prime factors between 3 and 7, i.e. they are co-prime. Hence, the HCF of 3 and 7 will be 1.

☛ Also Check:

HCF of 3 and 7 Examples

Example 1: Find the highest number that divides 3 and 7 exactly.

Solution:

The highest number that divides 3 and 7 exactly is their highest common factor, i.e. HCF of 3 and 7.
⇒ Factors of 3 and 7:
- Factors of 3 = 1, 3
- Factors of 7 = 1, 7
Therefore, the HCF of 3 and 7 is 1.
Example 2: For two numbers, HCF = 1 and LCM = 21. If one number is 7, find the other number.

Solution:

Given: HCF (z, 7) = 1 and LCM (z, 7) = 21
∵ HCF × LCM = 7 × (z)
⇒ z = (HCF × LCM)/7
⇒ z = (1 × 21)/7
⇒ z = 3
Therefore, the other number is 3.
Example 3: The product of two numbers is 21. If their HCF is 1, what is their LCM?

Solution:

Given: HCF = 1 and product of numbers = 21
∵ LCM × HCF = product of numbers
⇒ LCM = Product/HCF = 21/1
Therefore, the LCM is 21.

go to slide go to slide go to slide

Ready to see the world through math’s eyes?

Math is at the core of everything we do. Enjoy solving real-world math problems in live classes and become an expert at everything.

Book a Free Trial Class

FAQs on HCF of 3 and 7

What is the HCF of 3 and 7?

The HCF of 3 and 7 is 1. To calculate the HCF of 3 and 7, we need to factor each number (factors of 3 = 1, 3; factors of 7 = 1, 7) and choose the highest factor that exactly divides both 3 and 7, i.e., 1.

What is the Relation Between LCM and HCF of 3, 7?

The following equation can be used to express the relation between LCM and HCF of 3 and 7, i.e. HCF × LCM = 3 × 7.

How to Find the HCF of 3 and 7 by Long Division Method?

To find the HCF of 3, 7 using long division method, 7 is divided by 3. The corresponding divisor (1) when remainder equals 0 is taken as HCF.

If the HCF of 7 and 3 is 1, Find its LCM.

HCF(7, 3) × LCM(7, 3) = 7 × 3
Since the HCF of 7 and 3 = 1
⇒ 1 × LCM(7, 3) = 21
Therefore, LCM = 21
☛ Highest Common Factor Calculator

What are the Methods to Find HCF of 3 and 7?

There are three commonly used methods to find the HCF of 3 and 7.

By Prime Factorization
By Euclidean Algorithm
By Long Division

How to Find the HCF of 3 and 7 by Prime Factorization?

To find the HCF of 3 and 7, we will find the prime factorization of the given numbers, i.e. 3 = 3; 7 = 7.
⇒ There is no common prime factor for 3 and 7. Hence, HCF (3, 7) = 1.
☛ What are Prime Numbers?

Download FREE Study Materials

HCF and LCM

Math worksheets and
visual curriculum