A day full of math games & activities. Find one near you.

HCF of 12, 16 and 18

HCF of 12, 16 and 18 is the largest possible number that divides 12, 16 and 18 exactly without any remainder. The factors of 12, 16 and 18 are (1, 2, 3, 4, 6, 12), (1, 2, 4, 8, 16) and (1, 2, 3, 6, 9, 18) respectively. There are 3 commonly used methods to find the HCF of 12, 16 and 18 - prime factorization, long division, and Euclidean algorithm.

1.	HCF of 12, 16 and 18
2.	List of Methods
3.	Solved Examples
4.	FAQs

What is HCF of 12, 16 and 18?

Answer: HCF of 12, 16 and 18 is 2.

Explanation:

The HCF of three non-zero integers, x(12), y(16) and z(18), is the highest positive integer m(2) that divides x(12), y(16) and z(18) without any remainder.

Methods to Find HCF of 12, 16 and 18

The methods to find the HCF of 12, 16 and 18 are explained below.

Listing Common Factors
Prime Factorization Method
Using Euclid's Algorithm

HCF of 12, 16 and 18 by Listing Common Factors

Factors of 12: 1, 2, 3, 4, 6, 12
Factors of 16: 1, 2, 4, 8, 16
Factors of 18: 1, 2, 3, 6, 9, 18

There are 2 common factors of 12, 16 and 18, that are 1 and 2. Therefore, the highest common factor of 12, 16 and 18 is 2.

HCF of 12, 16 and 18 by Prime Factorization

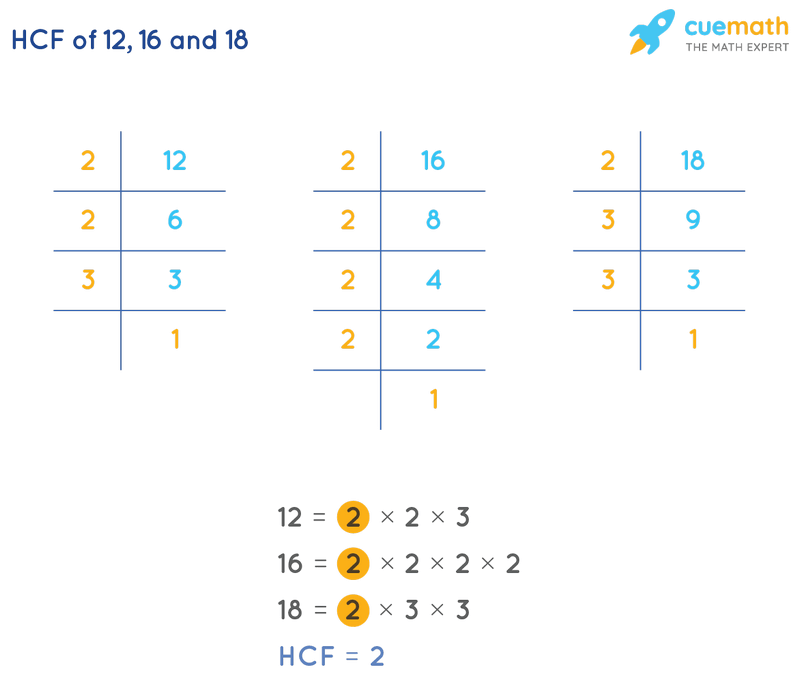
Prime factorization of 12, 16 and 18 is (2 × 2 × 3), (2 × 2 × 2 × 2) and (2 × 3 × 3) respectively. As visible, 12, 16 and 18 have only one common prime factor i.e. 2. Hence, the HCF of 12, 16 and 18 is 2.

HCF of 12, 16 and 18 by Euclidean Algorithm

As per the Euclidean Algorithm, HCF(X, Y) = HCF(Y, X mod Y)
where X > Y and mod is the modulo operator.

HCF(12, 16, 18) = HCF(HCF(12, 16), 18)

HCF(16, 12) = HCF(12, 16 mod 12) = HCF(12, 4)
HCF(12, 4) = HCF(4, 12 mod 4) = HCF(4, 0)
HCF(4, 0) = 4 (∵ HCF(X, 0) = |X|, where X ≠ 0)

Steps for HCF(4, 18)

HCF(18, 4) = HCF(4, 18 mod 4) = HCF(4, 2)
HCF(4, 2) = HCF(2, 4 mod 2) = HCF(2, 0)
HCF(2, 0) = 2 (∵ HCF(X, 0) = |X|, where X ≠ 0)

Therefore, the value of HCF of 12, 16 and 18 is 2.

☛ Also Check:

HCF of 12, 16 and 18 Examples

Example 1: Calculate the HCF of 12, 16, and 18 using LCM of the given numbers.

Solution:

Prime factorization of 12, 16 and 18 is given as,
- 12 = 2 × 2 × 3
- 16 = 2 × 2 × 2 × 2
- 18 = 2 × 3 × 3
LCM(12, 16) = 48, LCM(16, 18) = 144, LCM(18, 12) = 36, LCM(12, 16, 18) = 144
⇒ HCF(12, 16, 18) = [(12 × 16 × 18) × LCM(12, 16, 18)]/[LCM(12, 16) × LCM (16, 18) × LCM(18, 12)]
⇒ HCF(12, 16, 18) = (3456 × 144)/(48 × 144 × 36)
⇒ HCF(12, 16, 18) = 2.
Therefore, the HCF of 12, 16 and 18 is 2.
Example 2: Verify the relation between the LCM and HCF of 12, 16 and 18.

Solution:

The relation between the LCM and HCF of 12, 16 and 18 is given as, HCF(12, 16, 18) = [(12 × 16 × 18) × LCM(12, 16, 18)]/[LCM(12, 16) × LCM (16, 18) × LCM(12, 18)]
⇒ Prime factorization of 12, 16 and 18:
- 12 = 2 × 2 × 3
- 16 = 2 × 2 × 2 × 2
- 18 = 2 × 3 × 3
∴ LCM of (12, 16), (16, 18), (12, 18), and (12, 16, 18) is 48, 144, 36, and 144 respectively.
Now, LHS = HCF(12, 16, 18) = 2.
And, RHS = [(12 × 16 × 18) × LCM(12, 16, 18)]/[LCM(12, 16) × LCM (16, 18) × LCM(12, 18)] = [(3456) × 144]/[48 × 144 × 36]
LHS = RHS = 2.
Hence verified.
Example 3: Find the highest number that divides 12, 16, and 18 completely.

Solution:

The highest number that divides 12, 16, and 18 exactly is their highest common factor.
- Factors of 12 = 1, 2, 3, 4, 6, 12
- Factors of 16 = 1, 2, 4, 8, 16
- Factors of 18 = 1, 2, 3, 6, 9, 18
The HCF of 12, 16, and 18 is 2.
∴ The highest number that divides 12, 16, and 18 is 2.

go to slide go to slide go to slide

Ready to see the world through math’s eyes?

Math is at the core of everything we do. Enjoy solving real-world math problems in live classes and become an expert at everything.

Book a Free Trial Class

FAQs on HCF of 12, 16 and 18

What is the HCF of 12, 16 and 18?

The HCF of 12, 16 and 18 is 2. To calculate the highest common factor of 12, 16 and 18, we need to factor each number (factors of 12 = 1, 2, 3, 4, 6, 12; factors of 16 = 1, 2, 4, 8, 16; factors of 18 = 1, 2, 3, 6, 9, 18) and choose the highest factor that exactly divides 12, 16 and 18, i.e., 2.

Which of the following is HCF of 12, 16 and 18? 2, 44, 30, 20, 65

HCF of 12, 16, 18 will be the number that divides 12, 16, and 18 without leaving any remainder. The only number that satisfies the given condition is 2.

What is the Relation Between LCM and HCF of 12, 16 and 18?

The following equation can be used to express the relation between Least Common Multiple (LCM) and HCF of 12, 16 and 18, i.e. HCF(12, 16, 18) = [(12 × 16 × 18) × LCM(12, 16, 18)]/[LCM(12, 16) × LCM (16, 18) × LCM(12, 18)].
☛ HCF Calculator

How to Find the HCF of 12, 16 and 18 by Prime Factorization?

To find the HCF of 12, 16 and 18, we will find the prime factorization of given numbers, i.e. 12 = 2 × 2 × 3; 16 = 2 × 2 × 2 × 2; 18 = 2 × 3 × 3.
⇒ Since 2 is the only common prime factor of 12, 16 and 18. Hence, HCF(12, 16, 18) = 2.
☛ Prime Number

What are the Methods to Find HCF of 12, 16 and 18?

There are three commonly used methods to find the HCF of 12, 16 and 18.

By Listing Common Factors
By Long Division
By Prime Factorization

Download FREE Study Materials

HCF and LCM

Math worksheets and
visual curriculum