Geometric Probability
Geometric probability is the visual representation of probability. Many of the probabilities are continuous and for these probabilities, it is easy to represent as a geometric probability. The area of the geometric figure is used to compute the probabilities. The geometric probability is the probable area divided by the entire area.
Let us learn more about geometric probability and the representation of geometric probability with the help of examples, FAQs.
| 1. | What Is Geometric Probability? |
| 2. | Representation of Geometric Probability |
| 3. | Examples on Geometric Probability |
| 4. | Practice Questions |
| 5. | FAQs on Geometric Probability |
What Is Geometric Probability?
Geometric probability is the representation of probability geometrically. The probabilities which are non-discrete or are continuous are represented across a number line or across a two-dimensional plane. The experiment having numerous probability outcomes are often represented as a geometric probability.
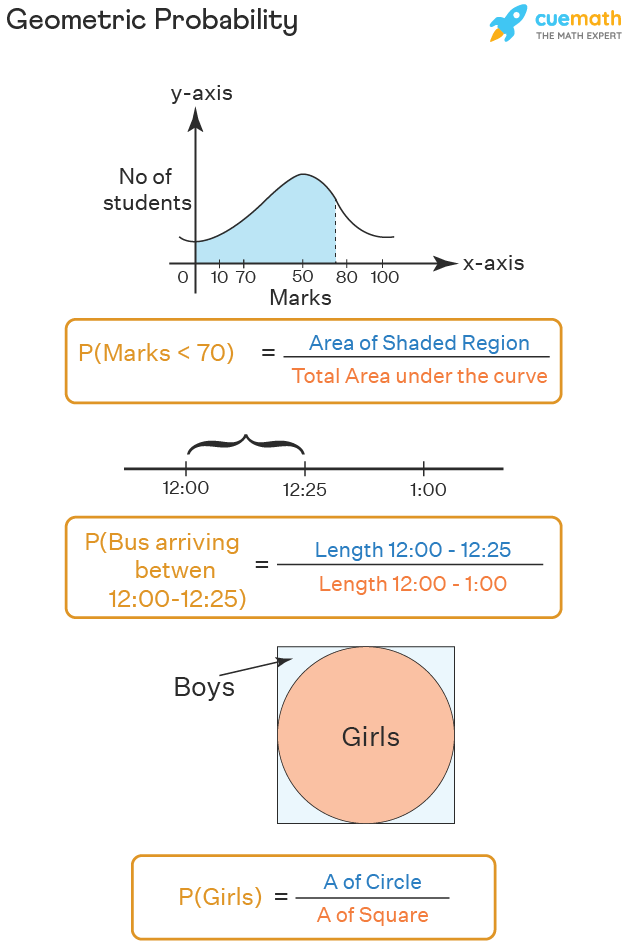
Probability is the mathematical way of calculating how likely a particular event may happen. Probability values always lie between 0 and 1,and sometimes they are also expressed as a percentage. The geometric probability is the representation of the probability as a form of a geometric figure such that the happening of an event is shaded as part of the area of the entire figure. We can assume geometric probability as a dartboard and the probability of hitting a particular area of the dartboard.
For calculation of geometric probability, we are only required to know the expected area where we want to hit with reference to the total area. Geometric probability is obtained by dividing the expected area by the total area.
Geometric Probability = Probable Area/Total Area
Geometric probability is also used to sometimes represent the different outcome probabilities at the same time. A few quick examples of geometric probability are as follows.
- The probability of the arrival of a train across a time period is a continuous probability, which can be represented as a geometric probability.
- In a class, the probability of a number of students gaining 65% or more marks can be represented as a geometric probability. This can be represented as a normal distribution, and the probability region can be shaded.
- Among a group of people, 30% drink tea, 40% drink coffee, and the remaining 30% drink soft drinks. This can be represented as a shaded region in a pi diagram.
- The probability of incidence of covid-19 among the population can be graphically represented as a geometric probability.
Representation of Geometric Probability
The geometric probabilities can be represented in a single dimension, two-dimensions, or n-dimensions, and can be represented as an area of the shaded probable region, with reference to the area of the entire region.
Number Line: The continuous probabilities are marked as a point on the number lines, and the length of the line from the starting point divided by the entire length of the line gives the probability answer.
Two Dimensional Plane: The geometric probability can be represented in the two-dimensional graph as a normal curve, as a pi diagram, or any other geometric shape. For the representation of the probability of a single event we use the normal curve, and represent the probability as the part of the area of the normal curve. And for representing multiple probabilities we use a Pi diagram or any other diagram. Further, we can represent geometric probability in higher dimensions also.
Percentage Format: Geometri probability is numerically represented as a percentage. The percentage value represents the happening of the event or the area of the geometric figure. 100% refers to the entire shaded image and it means the sure happening of the event. A 50% is represented as a half-shaded region and is equal to half of the chances of happening of an event.
☛Related Topics
FAQs on Geometric Probability
What Is Geometric Probability in Maths?
Geometric probability is the geometric or visual representation of probability in one, two or n-dimensional framework. The experiment having numerous probability outcomes are often represented as a geometric probability. For calculation of geometric probability, we are only required to know the expected area where we want to hit with reference to the total area. Geometric probability is obtained by dividing the expected area by the total area.
Geometric Probability = Probable Area/Total Area
Where Do We Use Geometric Probability?
The geometric probabilities are used if the range of probabilities is huge and it is difficult to represent it with a simple value. The geometric quantities of length, area, angle are used to express the probabilities of events.
What Are The Formulas Of Geometric Probability?
The formula of geometric probability is the expected area divided by the total area. We have Geometric Probability = Probable Area/Total Area. Also sometimes in place of area, we can also use the length, angle, or any other geometric quantity.
What Are The Examples Of Geometric Probability?
The examples of geometric probability include events that have a range of probabilities such as the probability of arrival of a bus across a time period. Also simple probabilities with multiple events can be represented as a geometric probability. If a party has people drinking tea, coffee, soft drink, milkshake, water, soda lime, then the probabilities can be easily represented using geometric probability.
What Is The Difference Between Geometric Probability And Discrete Probability?
The geometric probability is different from discrete probability, as the discrete probability has countable events which can be easily computed. The probabilities having continuous probabilities cannot be easily calculated and here we can use geometric probability. Probabilities involving dice, playing cards, coins are all simple examples of discrete probability, but probabilities involving student with a performance range, probabilities with time range can be represented using geometric probability.