GCF of 60 and 80
GCF of 60 and 80 is the largest possible number that divides 60 and 80 exactly without any remainder. The factors of 60 and 80 are 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60 and 1, 2, 4, 5, 8, 10, 16, 20, 40, 80 respectively. There are 3 commonly used methods to find the GCF of 60 and 80 - Euclidean algorithm, long division, and prime factorization.
| 1. | GCF of 60 and 80 |
| 2. | List of Methods |
| 3. | Solved Examples |
| 4. | FAQs |
What is GCF of 60 and 80?
Answer: GCF of 60 and 80 is 20.

Explanation:
The GCF of two non-zero integers, x(60) and y(80), is the greatest positive integer m(20) that divides both x(60) and y(80) without any remainder.
Methods to Find GCF of 60 and 80
Let's look at the different methods for finding the GCF of 60 and 80.
- Using Euclid's Algorithm
- Long Division Method
- Listing Common Factors
GCF of 60 and 80 by Euclidean Algorithm
As per the Euclidean Algorithm, GCF(X, Y) = GCF(Y, X mod Y)
where X > Y and mod is the modulo operator.
Here X = 80 and Y = 60
- GCF(80, 60) = GCF(60, 80 mod 60) = GCF(60, 20)
- GCF(60, 20) = GCF(20, 60 mod 20) = GCF(20, 0)
- GCF(20, 0) = 20 (∵ GCF(X, 0) = |X|, where X ≠ 0)
Therefore, the value of GCF of 60 and 80 is 20.
GCF of 60 and 80 by Long Division
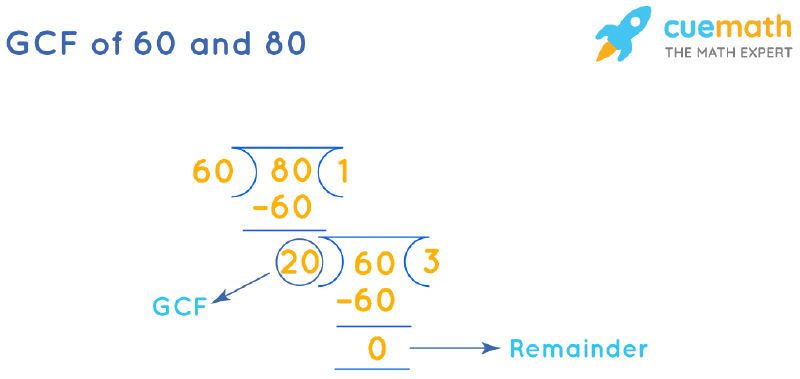
GCF of 60 and 80 is the divisor that we get when the remainder becomes 0 after doing long division repeatedly.
- Step 1: Divide 80 (larger number) by 60 (smaller number).
- Step 2: Since the remainder ≠ 0, we will divide the divisor of step 1 (60) by the remainder (20).
- Step 3: Repeat this process until the remainder = 0.
The corresponding divisor (20) is the GCF of 60 and 80.
GCF of 60 and 80 by Listing Common Factors
- Factors of 60: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60
- Factors of 80: 1, 2, 4, 5, 8, 10, 16, 20, 40, 80
There are 6 common factors of 60 and 80, that are 1, 2, 4, 5, 10, and 20. Therefore, the greatest common factor of 60 and 80 is 20.
☛ Also Check:
- GCF of 12 and 16 = 4
- GCF of 26 and 14 = 2
- GCF of 14 and 15 = 1
- GCF of 27 and 30 = 3
- GCF of 15 and 20 = 5
- GCF of 28 and 84 = 28
- GCF of 10 and 45 = 5
GCF of 60 and 80 Examples
-
Example 1: Find the GCF of 60 and 80, if their LCM is 240.
Solution:
∵ LCM × GCF = 60 × 80
⇒ GCF(60, 80) = (60 × 80)/240 = 20
Therefore, the greatest common factor of 60 and 80 is 20. -
Example 2: Find the greatest number that divides 60 and 80 exactly.
Solution:
The greatest number that divides 60 and 80 exactly is their greatest common factor, i.e. GCF of 60 and 80.
⇒ Factors of 60 and 80:- Factors of 60 = 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60
- Factors of 80 = 1, 2, 4, 5, 8, 10, 16, 20, 40, 80
Therefore, the GCF of 60 and 80 is 20.
-
Example 3: The product of two numbers is 4800. If their GCF is 20, what is their LCM?
Solution:
Given: GCF = 20 and product of numbers = 4800
∵ LCM × GCF = product of numbers
⇒ LCM = Product/GCF = 4800/20
Therefore, the LCM is 240.

FAQs on GCF of 60 and 80
What is the GCF of 60 and 80?
The GCF of 60 and 80 is 20. To calculate the GCF (Greatest Common Factor) of 60 and 80, we need to factor each number (factors of 60 = 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60; factors of 80 = 1, 2, 4, 5, 8, 10, 16, 20, 40, 80) and choose the greatest factor that exactly divides both 60 and 80, i.e., 20.
What is the Relation Between LCM and GCF of 60, 80?
The following equation can be used to express the relation between Least Common Multiple and GCF of 60 and 80, i.e. GCF × LCM = 60 × 80.
How to Find the GCF of 60 and 80 by Prime Factorization?
To find the GCF of 60 and 80, we will find the prime factorization of the given numbers, i.e. 60 = 2 × 2 × 3 × 5; 80 = 2 × 2 × 2 × 2 × 5.
⇒ Since 2, 2, 5 are common terms in the prime factorization of 60 and 80. Hence, GCF(60, 80) = 2 × 2 × 5 = 20
☛ Prime Number
If the GCF of 80 and 60 is 20, Find its LCM.
GCF(80, 60) × LCM(80, 60) = 80 × 60
Since the GCF of 80 and 60 = 20
⇒ 20 × LCM(80, 60) = 4800
Therefore, LCM = 240
☛ Greatest Common Factor Calculator
What are the Methods to Find GCF of 60 and 80?
There are three commonly used methods to find the GCF of 60 and 80.
- By Euclidean Algorithm
- By Long Division
- By Prime Factorization
How to Find the GCF of 60 and 80 by Long Division Method?
To find the GCF of 60, 80 using long division method, 80 is divided by 60. The corresponding divisor (20) when remainder equals 0 is taken as GCF.
visual curriculum
