A day full of math games & activities. Find one near you.

GCF of 11 and 12

GCF of 11 and 12 is the largest possible number that divides 11 and 12 exactly without any remainder. The factors of 11 and 12 are 1, 11 and 1, 2, 3, 4, 6, 12 respectively. There are 3 commonly used methods to find the GCF of 11 and 12 - prime factorization, Euclidean algorithm, and long division.

1.	GCF of 11 and 12
2.	List of Methods
3.	Solved Examples
4.	FAQs

What is GCF of 11 and 12?

Answer: GCF of 11 and 12 is 1.

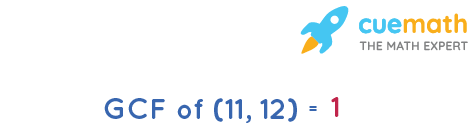
Explanation:

The GCF of two non-zero integers, x(11) and y(12), is the greatest positive integer m(1) that divides both x(11) and y(12) without any remainder.

Methods to Find GCF of 11 and 12

Let's look at the different methods for finding the GCF of 11 and 12.

Listing Common Factors
Long Division Method
Using Euclid's Algorithm

GCF of 11 and 12 by Listing Common Factors

Factors of 11: 1, 11
Factors of 12: 1, 2, 3, 4, 6, 12

Since, 1 is the only common factor between 11 and 12. The Greatest Common Factor of 11 and 12 is 1.

GCF of 11 and 12 by Long Division

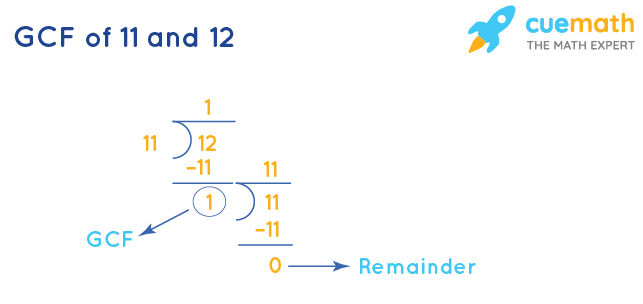
GCF of 11 and 12 is the divisor that we get when the remainder becomes 0 after doing long division repeatedly.

Step 1: Divide 12 (larger number) by 11 (smaller number).
Step 2: Since the remainder ≠ 0, we will divide the divisor of step 1 (11) by the remainder (1).
Step 3: Repeat this process until the remainder = 0.

The corresponding divisor (1) is the GCF of 11 and 12.

GCF of 11 and 12 by Euclidean Algorithm

As per the Euclidean Algorithm, GCF(X, Y) = GCF(Y, X mod Y)
where X > Y and mod is the modulo operator.

Here X = 12 and Y = 11

GCF(12, 11) = GCF(11, 12 mod 11) = GCF(11, 1)
GCF(11, 1) = GCF(1, 11 mod 1) = GCF(1, 0)
GCF(1, 0) = 1 (∵ GCF(X, 0) = |X|, where X ≠ 0)

Therefore, the value of GCF of 11 and 12 is 1.

☛ Also Check:

GCF of 11 and 12 Examples

Example 1: Find the GCF of 11 and 12, if their LCM is 132.

Solution:

∵ LCM × GCF = 11 × 12
⇒ GCF(11, 12) = (11 × 12)/132 = 1
Therefore, the greatest common factor of 11 and 12 is 1.
Example 2: For two numbers, GCF = 1 and LCM = 132. If one number is 11, find the other number.

Solution:

Given: GCF (x, 11) = 1 and LCM (x, 11) = 132
∵ GCF × LCM = 11 × (x)
⇒ x = (GCF × LCM)/11
⇒ x = (1 × 132)/11
⇒ x = 12
Therefore, the other number is 12.
Example 3: The product of two numbers is 132. If their GCF is 1, what is their LCM?

Solution:

Given: GCF = 1 and product of numbers = 132
∵ LCM × GCF = product of numbers
⇒ LCM = Product/GCF = 132/1
Therefore, the LCM is 132.

go to slide go to slide go to slide

Ready to see the world through math’s eyes?

Math is at the core of everything we do. Enjoy solving real-world math problems in live classes and become an expert at everything.

Book a Free Trial Class

FAQs on GCF of 11 and 12

What is the GCF of 11 and 12?

The GCF of 11 and 12 is 1. To calculate the greatest common factor of 11 and 12, we need to factor each number (factors of 11 = 1, 11; factors of 12 = 1, 2, 3, 4, 6, 12) and choose the greatest factor that exactly divides both 11 and 12, i.e., 1.

If the GCF of 12 and 11 is 1, Find its LCM.

GCF(12, 11) × LCM(12, 11) = 12 × 11
Since the GCF of 12 and 11 = 1
⇒ 1 × LCM(12, 11) = 132
Therefore, LCM = 132
☛ Greatest Common Factor Calculator

How to Find the GCF of 11 and 12 by Prime Factorization?

To find the GCF of 11 and 12, we will find the prime factorization of the given numbers, i.e. 11 = 11; 12 = 2 × 2 × 3.
⇒ There is no common prime factor for 11 and 12. Hence, GCF (11, 12) = 1.
☛ What are Prime Numbers?

What is the Relation Between LCM and GCF of 11, 12?

The following equation can be used to express the relation between LCM and GCF of 11 and 12, i.e. GCF × LCM = 11 × 12.

What are the Methods to Find GCF of 11 and 12?

There are three commonly used methods to find the GCF of 11 and 12.

By Prime Factorization
By Euclidean Algorithm
By Long Division

How to Find the GCF of 11 and 12 by Long Division Method?

To find the GCF of 11, 12 using long division method, 12 is divided by 11. The corresponding divisor (1) when remainder equals 0 is taken as GCF.

Download FREE Study Materials

GCF and LCM

Math worksheets and
visual curriculum