Factors of 36
Factors of 36 are those numbers that divide 36 completely without leaving any remainder. There are 9 factors of 36 among which 36 is the biggest factor and 2 and 3 are its prime factors. The prime factorization of 36 can be done by multiplying all its prime factors such that the product is 36. Let us learn how to write all the factors of 36, the prime factorization of 36, and the factor tree of 36 in this article.
| 1. | What are the Factors of 36? |
| 2. | Prime Factorization of 36 |
| 3. | Factor Tree of 36 |
| 4. | Factor Pairs of 36 |
| 5. | FAQs on Factors of 36 |
What are the Factors of 36?
The factors of 36 can be listed as 1, 2, 3, 4, 6, 9, 12, 18, and 36. According to the definition of factors, the factors of 36 are those numbers that divide 36 without leaving any remainder. In other words, we can say if two numbers are multiplied and the product is 36, then the numbers are the factors of 36. It means that 36 is completely divisible by all these numbers. Apart from these, 36 also has negative factors that can be listed as, -1, -2, -3, -4, -6, -9, -12, -18, and -36. For negative factors, we need to multiply a negative factor by a negative factor, like, (-12) × (-3) = 36.
How to Find the Factors of 36?
Factorization of a number means writing the number as a product of its factors. The most commonly used method to find the factors of a number is using the multiplication method. Let us find the factors of 36 using multiplication.
All Factors of 36 using Multiplication
Let us find all factors of 36 using the multiplication method using the following steps.
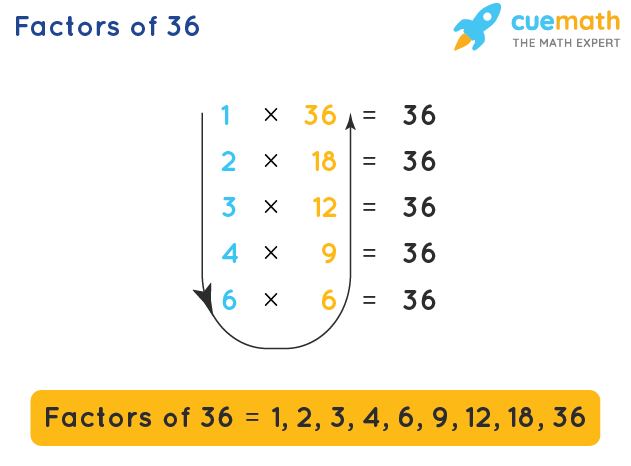
- Step 1: In order to find the factors of 36 using multiplication, we need to check what pairs of numbers multiply to get 36, so we need to divide 36 by natural numbers starting from 1 and go on till 9. We need to make a note of those numbers that divide 36 completely.
- Step 2: The numbers that completely divide 36 are known as its factors. We write that particular number along with its pair and make a list as shown in the figure given above. As we check and list all the numbers up to 9, we automatically get the other pair factor along with it. For example, starting from 1, we write 1 × 36 = 36, and 2 × 18 = 36, and so on. Here, (1, 36) forms the first pair, (2, 18) forms the second pair and the list goes on as shown. So, as we write 1 as the factor of 36, we get the other factor as 36; and as we write 2 as the factor of 36, we get 18 as the other factor. Like this, we get all the factors.
- Step 3: After the list is noted, we get all the factors of 36 starting from 1 up there, coming down and then we go up again up to 36. This gives us a complete list of all the factors of 36 as shown in the figure given above.
Therefore, the factors of 36 can be listed as 1, 2, 3, 4, 6, 9, 12, 18, and 36. Now, let us learn about the prime factorization of 36.
Prime Factors of 36
The prime factors of 36 are those factors of 36 that are prime numbers. The prime factors of 36 are different from the factors of 36. As we saw in the section above, the factors of 36 can be listed as 1, 2, 3, 4, 6, 9, 12, 18, and 36. However, all of these are not prime numbers. So, let us find the prime factors of 36 using prime factorization in the following section.
Prime Factorization of 36
Prime factorization is a way of expressing a number as a product of its prime factors. The prime factors of a number are those factors that are prime numbers. The prime factorization of 36 can be done using the following steps. Observe the figure given below to understand the prime factorization of 36.

- Step 1: The first step is to divide the number 36 with its smallest prime factor. We know that a prime factor is a prime number which is a factor of the given number. So, with the help of divisibility rules, we find out the smallest factor of the given number. Here, we get 2. Therefore, 2 is the smallest prime factor of 36. So, 36 ÷ 2 = 18
- Step 2: We need to repeatedly divide the quotient by 2 until we get a number that is no more divisible by 2. So, we divide 18 again by 2 which is 18 ÷ 2 = 9
- Step 3: Divide 18 again by 2 which results in 18 ÷ 2 = 9
- Step 4: Now, 9 is not completely divisible by 2, so, we proceed with the next prime factor of 36, which is 3. That is 9 ÷ 3 = 3
- Step 5: Divide the quotient by 3 again which is 3 ÷ 3 = 1
- Step 6: We need not proceed further as we have obtained 1 as our quotient.
- Step 7: Therefore, the prime factorization of 36 is expressed as 2 × 2 × 3 × 3 = 22 × 32; where 2 and 3 are prime numbers and the prime factors of 36.
Therefore, the prime factors of 36 are 2 and 3 and the Prime factorization of 36 = 2 × 2 × 3 × 3
Factor Tree of 36
We can also find the prime factors of 36 using a factor tree. The factor tree of 36 can be drawn by factorizing 36 until we reach its prime factors. These factors are split and written in the form of the branches of a tree. The final factors are circled and are considered to be the prime factors of 36. Let us find the prime factors of 36 using the following steps and the factor tree given below.

- Step 1: Split 36 into two factors. Let us take 2 and 18.
- Step 2: Observe these factors to see if they are prime or not.
- Step 3: Since 2 is a prime number we circle it as one of the prime factors of 36. We move on to 18, which is a composite number and further split it into more factors. In other words, we repeat the process of factorizing 18 and splitting it into branches until we reach a prime number.
- Step 4: Here, we get 2 and 9. So, we circle 2 because it is a prime number and we split 9 into 3 and 3. At this stage, we are left with prime numbers, 2 and 3. We circle them since we know that they cannot be factorized further. This is the end of the factor tree.
- Step 5: Therefore, the prime factors of 36 = 2 × 2 × 3 × 3
Note: It should be noted that there can be different factor trees of 36. For example, we can start by splitting 36 into 4 and 9. Then, 4 can be split further into 2 and 2, while 9 can be split into 3 and 3. Finally, we can observe the same prime factors, that is, 36 = 2 × 2 × 3 × 3
Factor Pairs of 36
The factors of 36 can be written in pairs. This means that the product of the pair factors of 36 is always 36. The factors of 36 in pairs can be written as shown in the table given below:
| Factors | Positive Pair Factors |
| 1 × 36 = 36 | 1, 36 |
| 2 × 18 = 36 | 2, 18 |
| 3 × 12 = 36 | 3, 12 |
| 4 × 9 = 36 | 4, 9 |
| 6 × 6 = 36 | 6, 6 |
It is possible to have negative pair factors as well because the product of two negative numbers also gives a positive number. Let us have a look at the negative pair factors of 36.
| Factors | Negative Pair Factors |
| -1 × -36 = 36 | -1, -36 |
| -2 × -18 = 36 | -2, -18 |
| -3 × -12 = 36 | -3, -12 |
| -4 × -9 = 36 | -4, -9 |
| -6 × -6 = 36 | -6, -6 |
The following points explain some features of the pair factors of 36.
- The pair factors of the number 36 are whole numbers in pairs that are multiplied to get the original number, i.e., 36.
- Pair factors could be either positive or negative but they cannot be fractions or decimal numbers.
- The positive pair factors of 36 are as follows: (1, 36), (2, 18), (3, 12), (4, 9), and (6, 6). The negative pair factors of 36 are (-1, -36), (-2, -18), (-3, -12), (-4, -9) and (-6, -6)
Important Notes
- Only composite numbers can have more than two factors. Since 36 is a composite number, it has more than two factors.
- Every factor of a given number is either less than or equal to the given number.
- The number of factors of a given number is finite. 36 has 9 factors.
- Factors of 36 are those numbers that divide 36 completely without leaving any remainder.
- 36 has a total of 9 factors: 1, 2, 3, 4, 6, 9, 12, 18, and 36.
- There is a trick to calculate the total number of factors of a number. For example, 36 = 2 × 2 × 3 × 3 = 22 × 32. We get the prime factorizations of 36 as 22 × 32. Just add one (1) to the exponents 2 and 2 individually and multiply their sums. (2 + 1) × (2 + 1) = 3 × 3 = 9. This means 36 has 9 factors in all.
Points to remember
Let us recollect the list of the factors, the negative factors, and the prime factors of 36.
- Factors of 36: 1, 2, 3, 4, 6, 9, 12, 24, and 36.
- Negative Factors of 36: -1, -2, -3, -4, -6, -9, -12, -18, and -36.
- Prime Factors of 36: 2, 3
- Prime Factorization of 36: 2 × 2 × 3 × 3 = 22 × 32
☛ Related Articles
- Factors of 33: The factors of 33 are 1, 3, 11, and 33.
- Factors of 34: The factors of 34 are 1, 2, 17, and 34.
- Factors of 38: The factors of 38 are 1, 2, 19, and 38.
- Factors of 30: The factors of 30 are 1, 2, 3, 5, 6, 10, 15, and 30.
- Factors of 360: The factors of 360 are 1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 18, 20, 24, 30, 36, 40, 45, 60, 72, 90, 120, 180, and 360.
- Factors of 35: The factors of 35 are 1, 5, 7, and 35.
- Factors of 37: The factors of 37 are 1 and 37.
Examples on Factors of 36
-
Example 1: State true or false with respect to the factors of 36.
a.) 3 and 6 are factors of 36.
b.) 2 and 3 are the prime factors of 36.
Solution:
a.) True, 3 and 6 are factors of 36.
b.) True, 2 and 3 are the prime factors of 36.
-
Example 2: Write all the positive factors of 36.
Solution:
All the positive factors of 36 are 1, 2, 3, 4, 6, 9, 12, 18, and 36.
-
Example 3:
List the positive and negative pair factors of 36.
Solution:
The positive pair factors of 36 are as follows: (1, 36), (2, 18), (3, 12), (4, 9), and (6, 6). The negative pair factors of 36 are (-1, -36), (-2, -18), (-3, -12), (-4, -9) and (-6, -6)

FAQs on Factors of 36
What are all the Factors of 36?
The factors of 36 are 1, 2, 3, 4, 6, 9, 12, 18, 36 and its negative factors are -1, -2, -3, -4, -6, -9, -12, -18, -36.
What are the Prime Factors of 36?
There are two prime factors of 36, and they are 2 and 3. The prime factors of a number are those factors that are prime numbers. In this case, if we do the prime factorization of 36, we get 2 × 2 × 3 × 3 = 22 × 32, where 2 and 3 are prime numbers and the prime factors of 36.
What are the Common Factors of 36 and 42?
The factors of 36 can be listed as 1, 2, 3, 4, 6, 9, 12, 18, 36 and the factors of 42 can be listed as 1, 2, 3, 6, 7, 14, 21, 42. Among these, we can list the common factors of 36 and 42 as 1, 2, 3, and 6. Now, we can find the Greatest Common Factor (GCF) of 36 and 42 which is 6.
What are the Common Factors of 36 and 40?
The factors of 36 can be listed as 1, 2, 3, 4, 6, 9, 12, 18, 36 and the factors of 40 can be listed as 1, 2, 4, 5, 8, 10, 20, 40. Among these, we can list the common factors of 36 and 40 as 1, 2, and 4. With the help of this, we can find the Greatest Common Factor (GCF) of 36 and 40 which is 4.
What is the Greatest Common Factor of 36 and 20?
The factors of 36 are 1, 2, 3, 4, 6, 9, 12, 18, 36 and the factors of 20 are 1, 2, 4, 5, 10, and 20. The Common factors of 36 and 20 are (1, 2, 4). Hence, the GCF of 36 and 20 is 4.
What is the Sum of all the Factors of 36?
The sum of all the factors of 36 can be calculated by adding 1, 2, 3, 4, 6, 9, 12, 18, 36 which is 1 + 2 + 3 + 4 + 6 + 9 + 12 + 18 + 36 = 91.
How many Factors does 36 have?
36 has a total of 9 factors that can be listed as, 1, 2, 3, 4, 6, 9, 12, 18, 36. However, the prime factors of 36 are 2 and 3.
What is the Prime Factorization of 36?
The prime factorization of 36 is expressed as follows: 36 = 2 × 2 × 3 × 3 = 22 × 32. It is to be noted that prime factorization is a way of expressing a number as a product of its prime factors. The prime factors of a number are those factors that are prime numbers. Here, 2 and 3 are prime numbers and the prime factors of 36.
visual curriculum