Factors of 2700 are integers that can be divided evenly into 2700. There are overall 36 factors of 2700 among which 2700 is the biggest factor and 2, 3, 5 are its prime factors. The Prime Factorization of 2700 is 2² × 3³ × 5².

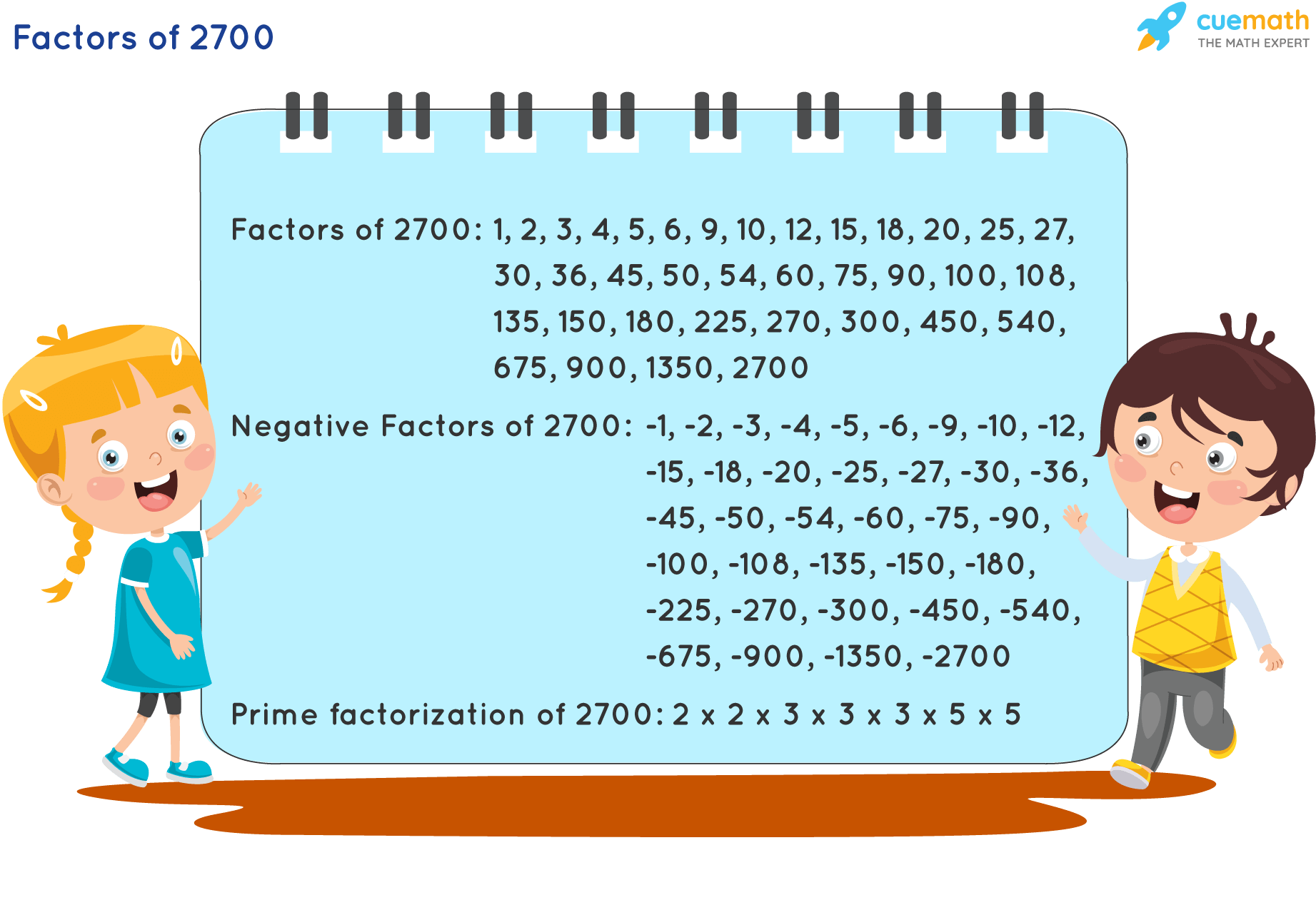
• All Factors of 2700: 1, 2, 3, 4, 5, 6, 9, 10, 12, 15, 18, 20, 25, 27, 30, 36, 45, 50, 54, 60, 75, 90, 100, 108, 135, 150, 180, 225, 270, 300, 450, 540, 675, 900, 1350 and 2700
• Prime Factors of 2700: 2, 3, 5
• Prime Factorization of 2700: 2² × 3³ × 5²
• Sum of Factors of 2700: 8680

1.	What Are the Factors of 2700?
2.	Factors of 2700 by Prime Factorization
3.	Factors of 2700 in Pairs
4.	FAQs on Factors of 2700

Factors of 2700 are pairs of those numbers whose products result in 2700. These factors are either prime numbers or composite numbers.

How to Find the Factors of 2700?

To find the factors of 2700, we will have to find the list of numbers that would divide 2700 without leaving any remainder.

• 2700/12 = 225; therefore, 12 is a factor of 2700 and 225 is also a factor of 2700.
• 2700/450 = 6; therefore, 450 is a factor of 2700 and 6 is also a factor of 2700.

Similarly we can find other factors. Hence, the factors of 2700 are 1, 2, 3, 4, 5, 6, 9, 10, 12, 15, 18, 20, 25, 27, 30, 36, 45, 50, 54, 60, 75, 90, 100, 108, 135, 150, 180, 225, 270, 300, 450, 540, 675, 900, 1350, 2700.

☛ Also Check:

• Factors of 50 - The factors of 50 are 1, 2, 5, 10, 25, 50
• Factors of 180 - The factors of 180 are 1, 2, 3, 4, 5, 6, 9, 10, 12, 15, 18, 20, 30, 36, 45, 60, 90, 180
• Factors of 21 - The factors of 21 are 1, 3, 7, 21
• Factors of 54 - The factors of 54 are 1, 2, 3, 6, 9, 18, 27, 54
• Factors of 10 - The factors of 10 are 1, 2, 5, 10

The number 2700 is composite and therefore it will have prime factors. Now let us learn how to calculate the prime factors of 2700. The first step is to divide the number 2700 with the smallest prime factor, here it is 2. We keep dividing until it gives a non-zero remainder.

• 2700 ÷ 2 = 1350
• 1350 ÷ 2 = 675

Further dividing 675 by 2 gives a non-zero remainder. So we stop the process and continue dividing the number 675 by the next smallest prime factor. We stop ultimately if the next prime factor doesn't exist or when we can't divide any further.

So, the prime factorization of 2700 can be written as 2² × 3³ × 5² where 2, 3, 5 are prime.

Pair factors of 2700 are the pairs of numbers that when multiplied give the product 2700. The factors of 2700 in pairs are:

• 1 × 2700 = (1, 2700)
• 2 × 1350 = (2, 1350)
• 3 × 900 = (3, 900)
• 4 × 675 = (4, 675)
• 5 × 540 = (5, 540)
• 6 × 450 = (6, 450)
• 9 × 300 = (9, 300)
• 10 × 270 = (10, 270)
• 12 × 225 = (12, 225)
• 15 × 180 = (15, 180)
• 18 × 150 = (18, 150)
• 20 × 135 = (20, 135)
• 25 × 108 = (25, 108)
• 27 × 100 = (27, 100)
• 30 × 90 = (30, 90)
• 36 × 75 = (36, 75)
• 45 × 60 = (45, 60)
• 50 × 54 = (50, 54)

Negative pair factors of 2700 are:

• -1 × -2700 = (-1, -2700)
• -2 × -1350 = (-2, -1350)
• -3 × -900 = (-3, -900)
• -4 × -675 = (-4, -675)
• -5 × -540 = (-5, -540)
• -6 × -450 = (-6, -450)
• -9 × -300 = (-9, -300)
• -10 × -270 = (-10, -270)
• -12 × -225 = (-12, -225)
• -15 × -180 = (-15, -180)
• -18 × -150 = (-18, -150)
• -20 × -135 = (-20, -135)
• -25 × -108 = (-25, -108)
• -27 × -100 = (-27, -100)
• -30 × -90 = (-30, -90)
• -36 × -75 = (-36, -75)
• -45 × -60 = (-45, -60)
• -50 × -54 = (-50, -54)

NOTE: If (a, b) is a pair factor of a number then (b, a) is also a pair factor of that number.