Factors and Multiples
Factors and multiples are related to each other. A factor of a number is the number that divides it completely without leaving any remainder. For any given number we can represent it as p × q = z. Here we say z is a multiple of p and q. According to the definition of factors and multiples, p and q are factors of z, because z is divisible by p as well as q. For example, 6 × 2 = 12, so 6 and 2 are the factors of 12, and 12 is a multiple of 6 and 2.
| 1. | How to Find Factors and Multiples? |
| 2. | Common Factors and Multiples |
| 3. | Properties of Factors and Multiples |
| 4. | FAQs on Factors and Multiples |
How to Find Factors and Multiples?
To find factors and multiples of any given number, let say 'p', we have to find the list of numbers that divide the number 'p' without leaving any remainder. Here let us take an example of number 28. How can we find factors of 28?
Steps to Find Factors of a Number
- Step 1: List the two numbers such that their product gives 28.
- Step 2: Let's say we take 4 and 7 as the numbers.
- Step 3: Here 28 is divisible by 4 and 7 without leaving any remainder.
- Step 4: Hence, 28 can be factored in as 28 = 7 × 4.
- Step 5: Further, there are finite numbers by which a number can be divided without leaving any remainder. List out the numbers. Here, in the case of 28, the numbers are 1, 2, 4, 7, 14, and 28.
- Step 6: Factors of 28 can be listed as 1, 2, 4, 7, 14, and 28.
1 and the number itself are always the factors of the respective number.
Finding Multiples of a Number
Multiples of a number are the numbers that we get after multiplying the number by a whole number. Here, let us take the same example of number 28. How can we find multiples of 28? The multiples of 28 are all the numbers that result from the multiplication of 28 by another whole number. Let us look at the skip counting method shown in the image below. The skip counting method is one of the simplest methods to find the multiples of any given number.
| Multiples of 28 | Explanation |
|---|---|
| 28 | 28 × 1 |
| 56 | 28 × 2 or 28 + 28 |
| 84 | 28 × 3 or 28 + 28 + 28 |
| 112 | 28 × 4 or 28 + 28 + 28 + 28 |
| 140 | 28 × 5 or 28 + 28 + 28 + 28 + 28 |
| 168 | 28 × 6 or 28 + 28 + 28 + 28 + 28 + 28 |
Here, 28, 56, 84, 112, 140, and 168 are a few multiples of 28. There are infinite multiples of any given number.
Common Factors and Multiples
In this section, you will learn how to find common factors and multiples of any number. We know that a factor is a number that exactly divides the given number. Hence, a factor is nothing but a divisor of the given number. To find the factors, we can use the multiplication as well as the division method. To check if two or more numbers have common factors between them we can follow the below steps:
- Write the given numbers.
- Write all the possible factors of the given numbers
- Find the factors which are the same in both the numbers.
- Encircle the common factors.
This way we can easily find common factors between two or more numbers. Let us look at some examples.
Common factors of 30 and 42:
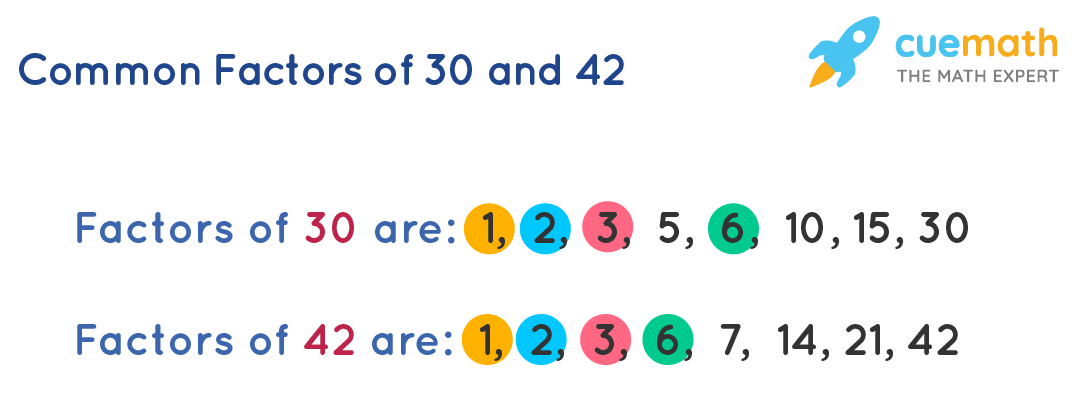
Therefore, the common factors of 30 and 42 are 1, 2, 3, and 6.
Here is another example with three numbers. The common factors of 42, 70, and 84 are shown in the image below.

Hence the common factors of 42, 70, and 84 are 1, 2, 7, and 14. Now let us look at ways to find common multiples.
There are various methods to find common multiples. Two of such ways are:
- Listing multiples method. In this, we list the multiples of each number and then we find their common multiples. It is one of the simplest methods by which we can find the common multiples of two or more numbers.
- Venn diagram method
Let us use the Venn diagram method. First, mark the multiples of any 2 numbers, let's say 3 and 4 in two separate circles. Look for the common numbers coming in both circles. The circle of multiples of 3 intersects with the circle of multiples of 4. The intersection part has the common multiples that belong to 3 as well as 4. Please note that there are infinite numbers of common multiples for every pair of numbers. The first three common multiples of 3 and 4 are 12, 24, and 36.

Now, let us look at an example of the listing multiples method. To find the common multiples of 2 and 4, we list their multiples and then find their common multiples.
- Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20. 22, 24, etc.
- Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, etc.
- Common multiples of 2 and 4: 4, 8, 12, 16, 20, 24, etc …
If a number is a factor of another number, then their common multiples are all the multiples of the larger number (as in the above example).
Properties of Factors and Multiples
There are many properties of factors and multiples that will help you to understand this concept properly. Those properties are listed below:
- 1 is the factor of every number.
- 0 is the multiple of every number.
- Factors and multiples are only used and applicable to whole numbers.
- For every number, 1 is the smallest factor and that number itself is the largest factor.
- Every number is a multiple of itself.
- There are an infinite number of multiples and a finite number of factors possible for every number.
- If there are only two factors of a number, i.e 1 and the number itself, that number is known as a prime number in math.
Important Notes
- Multiples of any number are infinite. Therefore, a set of any two numbers can have an infinite number of common multiples.
- The Least Common Multiple (LCM) is the smallest common multiple of sets of any two or more numbers. For example, the LCM of 3 and 4 is 12.
Related Articles on Factors and Multiples
Check these interesting articles related to the concept of factors and multiples grade 5.
Examples of factors and Multiples
-
Example 1: Find all the numbers which are less than 100 and are common multiples of 3 and 4?
Solution:
As per the definition of common factors and multiples, the common multiples of 3 and 4 are equal to the multiples of LCM of 3 and 4. The LCM of 3 and 4 is 12. All the multiples of 12 which are less than 100 are 12, 24, 36, 48, 60, 72, 84, and 96.
Therefore, the common multiples of 3 and 4 are 12, 24, 36, 48, 60, 72, 84, and 96. -
Example 2: What are the factors and multiples of 60?
Solution:
The factors of 60 are all the whole numbers that can divide 60 without leaving any remainder. So, the factors of 60 are 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 and 60. The mutiples of 60 can be found by multiplying 60 with whole numbers starting from 1.
60 × 1 = 60
60 × 2 = 120
60 × 3 = 180
60 × 4 = 240
60 × 5 = 300
So, the list of multiples of 60 includes 60, 120, 180, 240, 300, and so on.
Therefore, the factors and multiples of 60 are:
Factors = 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 and 60
Multiples = 60, 120, 180, 240, 300, ... -
Example 3: Find the common factors and multiples of 4, 8, and 12.
Solution: To find the common factors and multiples of 4, 8, and 12 we will use the listing method.
Let us write separately factors of 4,8 and 12. There are 3 factors of 4 which are 1, 2, and 4. There are 4 factors of 8 listed as 1, 2, 4, and 8. There are 6 factors of 12 which are 1, 2, 3, 4, 6, and 12.
The common factors of 4, 8, and 12 are 1, 2, and 4.
Let us make a list of multiples of 4, 8, and 12.
Multiples of 4 = 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60, 64, 68, 72 ...
Multiples of 8 = 8, 16, 24, 32, 40, 48, 56, 64, 72, 80 ...
Multiples of 12 = 12, 24, 36, 48, 60, 72, ...
So, the common multiples of 4, 8, and 12 are 24, 48, 72, ...

FAQs on Factors And Multiples
What are Factors and Multiples?
Factors and multiples are two related concepts in math. A factor is a number that divides the given number exactly with 0 as the remainder. And a multiple is a number that is obtained by multiplying the given number with any whole number. For example, if it is given that 5 × 6 = 30. Here, 30 is the multiple of 5 and 6, and 5, and 6 are the factors of 30.
What are the Factors and Multiples of 4?
The factors of 4 are 1, 2, and 4. And the multiples of 4 include 4, 8, 12, 16, 20, etc.
What is the Relationship Between Factors and Multiples?
The relationship between factors and multiples is that if we express it in the form of a multiplication fact "p × q = r", then the p and q represent the factors of the product. The product 'r' is the multiple of p and q.
What is the Difference Between Factors and Multiples of a Number?
The differences between factors and multiples are given below:
- Factors of a number are always less than or equal to the given number. While multiples of a number are always equal to or greater than the given number (except 0).
- A factor is a quantity in which we are dividing the given quantity, while multiple is the quantity that we are dividing into smaller units.
How to Teach Factors and Multiples to 4th Grade?
There are many activities and games for teaching factors and multiples to fourth graders. The activities are listed below:
- Play clap activity with learners. Choose any number, let's say 5, and ask learners to start counting from 1 such that one person will speak out one number only at their turn. Then, whoever will have the number 5 or multiples of 5 will not say the number. Instead, they have to clap one time. This way, we will get multiples of 5.
- Give factors and multiples worksheets to learners.
How do you Use Factor and Multiples?
Factors and multiples are very commonly and actively used in mathematics. So, it is important to understand this concept in detail. It is used in division, measurements, patterns, etc.
What is a Factors and Multiples Formula?
An equation that represents both factors and multiples of a number is a × b = c, where c represents the multiple of a and b, and a, and b are the factors of c.
What are Common Factors and Multiples?
Common factors and multiples can be found using the listing method or by using prime factorization method. A common factor of two or more numbers is the number that can divide all those numbers excatly without leaving any remainder. For example, 1 and 5 are the common factors are 5, 15, and 25. A common multiple is a number that comes in the multiplication table of more than two numbers and hence, it is said to be the common multiple of the respective numbers. For example, the first two common multiples of 3 and 5 are 15 and 30.
visual curriculum
