Dividing Mixed Fractions

Dividing mixed fractions is the division operation carried out between two mixed fractions. It is similar to the multiplication operation by taking the inverse of the second fraction. We will be learning about the steps of dividing mixed fractions along with examples in this article.

As we know, the term 'like denominators' means the denominators are the same. Hence, we will be taking mixed numbers with like denominators to understand the steps with an example.

Let us go through the following important points that will help you while dividing mixed fractions.

• A mixed fraction \(a\dfrac{b}{c}\) can also be written as a + (b/c) and vice-versa.
• To convert a mixed number to an improper fraction, the whole number is multiplied by the denominator and the result is added to the numerator of the proper fraction by retaining the denominator. For example, to convert \(2\dfrac{1}{7}\) to an improper fraction, we multiply 2 and 7 i.e, 2 × 7 = 14 and the result is added to 1 i.e., 14 + 1 = 15. Thus the improper fraction is 15/7.
• To convert an improper fraction to a mixed number we will divide the numerator of the improper fraction by its denominator. The quotient becomes the whole number part, the remainder becomes the numerator of the proper fraction and the denominator remains as it is. For example, to convert 21/4 to a mixed number, we first divide 21 by 4 and get the quotient as 5 and the remainder as 1. Thus, the mixed number is \(5\dfrac{1}{4}\).

Now, we will be taking an example to understand the steps of dividing mixed numbers with like denominators.

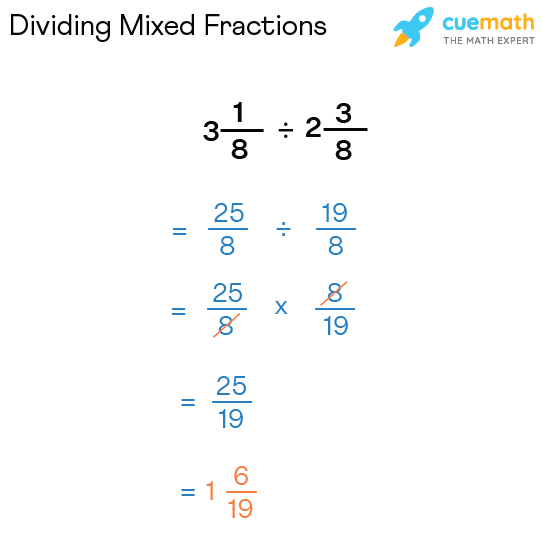
Example: Divide the mixed fraction \(3\dfrac{1}{8}\) by \(2\dfrac{3}{8}\).

We have to perform \(3\dfrac{1}{8}\) ÷ \(2\dfrac{3}{8}\).

• Step 1: Convert the given mixed fractions to improper fractions. i.e., \(3\dfrac{1}{8}\) = 25/8 and \(2\dfrac{3}{8}\) = 19/8.
• Step 2: We will multiply the reciprocal of the second fraction with the first fraction, i.e., (25/8) × (8/19).
• Step 3: The numerators and denominators of these fractions are multiplied separately. i.e., (25 × 8) / (8 × 19).
• Step 4: Cancel out the common factors if they exist in the numerator and the denominator. We cancel out 8.
• Step 5: Perform the calculation. We get 25/19.
• Step 6: If the result obtained in the previous step is an improper fraction, convert it to a mixed number, i.e., 25/19 = \(1\dfrac{6}{19}\).

Dividing mixed fractions with unlike denominators is defined as the division of mixed fractions with different denominators. The steps to perform the division remains the same as described in the previous section. Let us take an example to understand the division of mixed fractions with unlike denominators.

Example: Divide the mixed fraction \(2\dfrac{2}{9}\) by \(3\dfrac{1}{7}\).

We have to perform the calculation \(2\dfrac{2}{9}\) ÷ \(3\dfrac{1}{7}\). On converting the mixed fractions \(2\dfrac{2}{9}\) and \(3\dfrac{1}{7}\) to improper fractions we get 20/9 and 22/7 respectively.

We will now divide (20/9) by (22/7).

= (20/9) ÷ (22/7)

= (20/9) × (7/22)

= (10 × 7) / (9 × 11) (By canceling 2 from the numerator and the denominator)

= 70/99

Thus, the result of the calculation \(2\dfrac{2}{9}\) ÷ \(3\dfrac{1}{7}\) is 70/99.

Whole numbers can be expressed as fractions by considering the denominator to be 1. For example, 9 can be written as 9/1. To divide mixed fractions by whole numbers, we will convert the mixed fraction to an improper fraction and represent the whole number as a fraction followed by the steps of dividing mixed fractions as described in the previous section. Let's take an example to understand this.

Example: Divide the mixed fraction \(4\dfrac{1}{5}\) by the whole number 7.

We have to perform the calculation \(4\dfrac{1}{5}\) ÷ 7. On converting the mixed fraction \(4\dfrac{1}{5}\) to improper fraction we get 21/5 and the whole number 7 can be written as 7/1.

We will now divide (21/5) by (7/1).

= (21/5) ÷ (7/1)

= (21/5) × (1/7)

= (21 × 1) / (5 × 7)

= 3/5

Therefore, the result of \(4\dfrac{1}{5}\) ÷ 7 is 3/5.

Dividing mixed fractions with fractions is defined as the division performed between a mixed fraction and a proper fraction. The steps to divide them will remain the same as discussed earlier. We will convert the mixed fraction to an improper fraction, followed by dividing the same by the given fraction by following the steps of division. Let's take an example to understand this.

Example: Divide the mixed fraction \(5\dfrac{2}{3}\) by the fraction 2/9.

We will convert the mixed fraction \(5\dfrac{2}{3}\) to an improper fraction. On converting \(5\dfrac{2}{3}\) to an improper fraction we get 17/3. We will now divide (17/3) by (2/9).

(17/3) ÷ (2/9)

= (17/3) × (9/2)

= (17 × 9) / (3 × 2)

= (17 × 3) / 2

= 51/2

= \(25\dfrac{1}{2}\)

Thus, the value of \(5\dfrac{2}{3}\) ÷ (2/9) is \(25\dfrac{1}{2}\).

Related Articles

Check these articles related to the concept of dividing mixed fractions.

• Mixed fractions
• Improper fractions
• Proper fraction
• Fractions

What is Dividing Mixed Fractions?

Dividing mixed numbers are defined as the division of two mixed numbers such as \(2\dfrac{2}{9}\) ÷ \(3\dfrac{1}{7}\) wherein the mixed numbers are converted to improper fractions first and then they are divided.

How to Solve Dividing Mixed Fractions?

To solve dividing mixed fractions, the mixed fractions are first converted into improper fractions, followed by taking the reciprocal of the second fraction, and then the resultant fractions are multiplied. The result is further simplified to its lowest form by canceling out the common terms if they exist.
For example,
\(2\dfrac{1}{7}\) ÷ \(3\dfrac{5}{7}\)
= (15/7) ÷ (26/7)
= (15/7) × (7/26)
= 15/26

What are the Steps of Dividing Mixed Fractions?

The steps to divide the mixed numbers are as follows:

• Step 1: The given mixed numbers are converted to improper fractions.
• Step 2: The reciprocal of the second fraction is found.
• Step 3: The two fractions are now multiplied.
• Step 4: They are further simplified to get the lowest form.
• Step 5: If the result is an improper fraction, then it is again converted to a mixed fraction.

What is the First Step when Dividing Mixed Fractions?

The first step when dividing mixed numbers is to convert the given mixed fractions into improper fractions followed by the further steps of division. For example, to perform \(4\dfrac{2}{3}\) ÷ \(3\dfrac{1}{3}\), the first step is to convert the given mixed numbers to improper fractions, i.e., \(4\dfrac{2}{3}\) = 14/3 and \(3\dfrac{1}{3}\) = 10/3.

How to Divide Mixed Fractions by Whole Numbers?

To divide mixed numbers by whole numbers, we convert the given mixed fraction to an improper fraction. We now write the whole number in the form of a fraction by making the denominator as 1. Now, by taking the reciprocal of the whole number we multiply it with the first fraction and simplify the obtained result to get the lowest form of the result.

How to Divide Mixed Fractions with Different Denominators?

Dividing mixed fractions with different denominators can easily be done just like the regular division of mixed fractions. For this, the mixed fractions will be converted to improper fractions initially. The reciprocal of the second fraction is taken. Next, the numerator of these improper fractions will be multiplied. The denominators will also be multiplied. The result will be further simplified to obtain the final answer.
For example, \(3\dfrac{1}{4}\) ÷ \(3\dfrac{1}{3}\)
= (13/4) ÷ (10/3)
= (13/4) × (3/10)
= (13 × 3) / (4 × 10)
= 39/40

How to Divide Mixed Numbers by Fractions?

For dividing mixed fractions by fractions, we first convert the mixed fraction to an improper fraction followed by taking the reciprocal of the second fraction and multiplying the two fractions and simplifying them.