Base
Base, in math, is defined as a set of digits used to represent numbers. Different number systems use different combinations of digits as the base. For example, the binary number system uses only 2 digits, i.e., 0 and 1 to represent numbers, the Octal number system uses 8 digits, i.e., 0 to 7, to represent numbers, and so on. The most common number system that we use is the decimal number system that uses the base 10, which includes digits from 0 to 9 for writing numbers.
Any real number 'n' can be converted to a different base number system. For example, if we have to convert 12 to base 10, we just have to multiply the digits starting from the unit place by the whole number exponents of 10. So, 12 will become (2×100) + (1×101), which is 2+10=12.
What is Base?
The word "base" has different meanings in various contexts. In general, the term "base" defines the starting point, a fundamental part, or a bottom layer of something that provides support. A number system is essential to represent or denote numbers. Base refers to the digits that form a building block for expressing numbers. These sets of digits or alphabets make the base of a number system. Binary, decimal, octal, and hexadecimal are a few popular number systems with different bases.
Base Definition: Base, in math, is defined as the total count of digits used to express numbers in a number system. The base of a number system is also referred to as "radix." There are many number systems and each one of them has different bases. Numbers in a base start from 0. The most commonly and widely used bases are binary number system (Base-2), octal number system (Base-8), decimal number system (Base-10), and hexadecimal number system (base-16).
Let's look at the mathematical terms for each of the known number systems through the table given below.
| Number System | Base |
|---|---|
| Binary | 2 |
| Ternary | 3 |
| Quaternary | 4 |
| Quinary | 5 |
| Senary | 6 |
| Septenary | 7 |
| Octal | 8 |
| Nonary | 9 |
| Decimal | 10 |
| Undecimal | 11 |
| Duodecimal | 12 |
| Hexadecimal | 16 |
| Vigesimal | 20 |
| Sexagesimal | 60 |
Among these, there are four popular number systems that we are going to study in detail in this article.
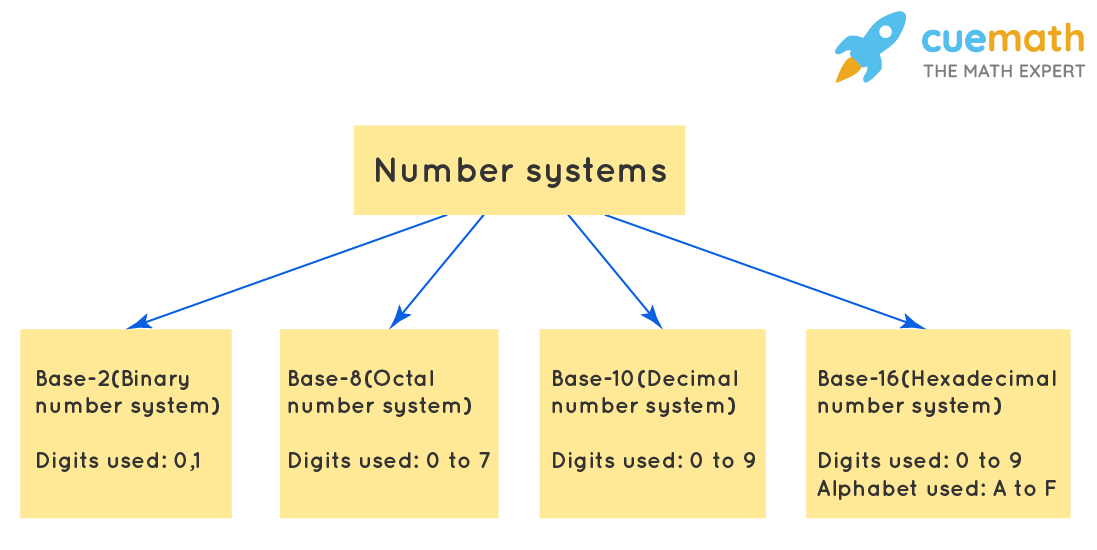
Let's understand each of these four base systems in detail.
Base-2 (Binary Number System)
Base-2 number system uses only 2 digits (0 and 1). Since there are only 2 digits involved in representing any number, it is called the base-2 number system. This system of base is used in computers to store and process data. The digits 0 and 1 are called binary digits or BITS, in the abbreviated form. Subscript 2 is used to identify a base-2 number. Let's see how to convert \(101_{2}\) to the decimal number system with the help of this example, \(101_{2}\) = (1 × 20) + (0 × 21) + (1 × 22) = 5.

Decimal Numbers And Their Corresponding Binary Equivalents
Binary numbers are represented as shown in the following table. Each digit is multiplied by the power of 2 based on its position (the position starts from right to left) and the products are added. Some examples of binary numbers are \(1101_{2}\), \(1100_{2}\), \(10111_{2}\), etc.
| Decimal Number | Binary Equivalent |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 10 |
| 3 | 11 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
| 8 | 1000 |
| 9 | 1001 |
| 10 | 1010 |
Base-8 (Octal Number System)
Base-8 number system uses only 8 digits ranging from 0 to 7. Since there are 8 distinct digits used to express a number, the base of this number system is 8. Octal numbers are represented using 3 digits (composed of 0s and 1s). The octal number system uses a lesser number of digits compared to many other number systems, so there are fewer computational errors. The subscript 8 is used to identify the base-8 number. An example of a number in octal number system is \(423_{8}\) = (3 × 80) + (2 × 81) + (4 × 82).

Decimal Numbers and Their Corresponding Octal Equivalents
| Decimal Number | Octal Equivalent |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
| 6 | 6 |
| 7 | 7 |
| 8 | 10 |
| 9 | 11 |
| 10 | 12 |
| 11 | 13 |
| 12 | 14 |
| 13 | 15 |
| 15 | 16 |
An octal number is represented as shown in the table above. Each digit is multiplied by the power of 8 based on its position (position starts from right to left) and the products are added.
Base-10 (Decimal Number System)
Base-10 number system uses only digits from 0 to 9. Since there are only ten digits involved in representing any number, it is called base-10 or the decimal number system. It is one of the most commonly used number systems around the world. Let us see how we count in the base-10 number system. The subscript 10 is used to identify a base-10 number. For example, \(743_{10}\) = (3 × 100) + (4 × 101) + (7 × 102). Generally, we do not write 10 as the subscript to represent the decimal number system. So, if you see any number without any subscript written, it is a base-10 number.

A decimal number is represented as shown in the table above. Each digit is multiplied by the power of 10 based on its position (position starts from right to left) and the products are added. Let us look into how numbers are formed in the (base-10) decimal number system. We start counting from 0 to 9. Now that we have used all the digits and there is no other number to express ten. At this point, we begin from the first. But, we cannot use 0 again to represent 10. So, we add a '1' in front of 0 and make it 10. The consecutive numbers can be obtained by adding a '1' before 1, 2, 3, 4, 5, 6, 7, 8, 9. The same rule holds good for every next set of ten numbers.
Please observe the table below to see how the base 10 (decimal numbers) are formed.
Numbers in Decimal Number System
| Set of Numbers | Their Numerical Equivalent |
|---|---|
| First ten numbers | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 |
| Second ten numbers | 10, 11, 12, 13, 14, 15, 16, 17, 18, 19 (Begin to count from 0 to 9 but add a '1' before all the numbers from 0 to 9) |
| Third ten numbers | 20, 21, 22, 23, 24, 25, 26, 27, 28, 29 (Begin to count from 0 to 9 but add a '2' before all the numbers from 0 to 9) |
| Fourth ten numbers | 30, 31, 32, 33, 34, 35, 36, 37, 38, 39 (Begin to count from 0 to 9 but add a '3' before all the numbers from 0 to 9) |
Base-16 (Hexadecimal Number System)
The base-16 number system uses numbers and alphabets to represent numbers. Numbers from 0 to 9 and alphabets from A to F are used. It takes 4 bits (composed of 0s and 1s) to represent any digit. The base-16 system is used in computers and digital systems to store very large numbers. It is also used to represent colors in computers.

Let us look at the representation of hexadecimal digits. We start to count from 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 1A, 1B, 1C, 1D, 1E, 1F, etc. Here, 10 does not refer to the number after 9 but it is 1-0, which means that there is 1 group of 16 numbers starting from 0 to 9 and A to F and there are no more leftover numbers. For example, \(6AB_{16}\) = (11 × 160) + (10 × 161) + (6 × 162)
Decimal Numbers and Their Corresponding Hexadecimal Equivalents
A hexadecimal number is represented as shown in the following table. Each digit is multiplied by the power of 16 based on its position (the position starts from right to left) and the products are added.
| Decimal Number | Hexadecimal Equivalent |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
| 6 | 6 |
| 7 | 7 |
| 8 | 8 |
| 9 | 9 |
| 10 | A |
| 11 | B |
| 12 | C |
| 13 | D |
| 14 | E |
| 15 | F |
Base of a Number System
The base of a number system is a whole number that represents a count of different numbers of digits and alphabets (used in base 16, hexadecimal number system) used to denote any number. A number can be represented as the sum of the base with various exponents.
Related Articles on Base
Check out these interesting articles on base. Click on any of these to know more!
- Binary to Decimal Calculator
- Decimal to Binary Calculator
- 12 in Binary
- 42 in Binary
- 64 in Binary
- 255 in Binary
- 15 In Binary
- 32 in Binary
- 100 In Binary
- 22 In Binary
- 16 in Binary
- 128 in Binary
- Decimal to Hexadecimal Conversion Formula
How to Show the Base?
We can show the base of a number by adding a subscript (the number base represented beside the given number in a smaller size) to the number. Let us see how we can express a decimal number that has a base of 10.
34510 represents the number 345 with base 10 (it is read as 345 base 10).
To express a number in a particular base, we consider the following.
- The number
- The position of the number put in the superscript of the base number.
- The base
Decimal number 345 can be expressed in base 10 as follows, (3 × 102) + (4 × 101) + (5 × 100) (three hundreds, four tens, and five ones. 100 denotes a value of 1). Similarly, \(110_{2}\) represents the number 110 with base 2 (it is read as 110 base 2). This number can be expressed as \(110_{2}\) = (0 × 20) + (1 × 21) + (1 × 22)
Facts About Base in Math
Listed below are some important facts related to base:
- The most commonly and widely used number system around the world is the base 10 or the decimal number system.
- A base 10 number can be converted to any other number system of a different base and vice versa.
- Computers understand all the inputs given to them as numbers. They are either 0 or 1, which form the base-2 or binary number system.
- Octal and hexadecimal number systems are also used in computers to represent large numbers and words.
- The other types of base in math number systems are mentioned in the table below.
Other Number Systems With Their Bases and Digits
| Base Name | Radix (Base Number) |
|---|---|
| Ternary | Base-3 (Has digits 0, 1, 2) |
| Quaternary | Base-4 (Has digits 0, 1, 2, 3) |
| Quinary | Base-5 (0, 1, 2, 3, 4) |
| Senary | Base-6 (0, 1, 2, 3, 4, 5) |
| Septenary | Base-7 (Has digits 0, 1, 2, 3, 4, 5, 6) |
| Nonary | Base-9 (Has digits 0, 1, 2, 3, 4, 5, 6, 7, 8) |
Important Notes:
Read the given important notes related to the base of a number.
-
The base of a number system is called "radix."
-
A number in a base can be written as the number with the base number as a subscript. (Numberbase).
-
Computers use different bases (binary, octal, hexadecimal).
-
The decimal number system (base-10) is the most commonly used number system.
Tips and Tricks:
Given below are some tips and tricks related to the base of a number:
- A number in one base can be converted to a number in any other base.
- To convert a number from the binary/octal/hexadecimal system to the decimal system, we multiply each digit of the given number with exponents of the base based on their position from right to left. The positions start from 0 and increase as they move to the right. We then simplify and add the expressions.
- To convert a decimal number to a binary/octal/decimal number system, we continuously divide the given number with the base of the required number until we arrive at a number lesser than the base of the number system to be converted. We then arrange the remainders of all the divisions in the bottom-to-top direction to express the number.
Solved Examples on Base
-
Example 1: Convert \(153_{10}\) to base-2 number system.
Solution: Start dividing 153 by 2 repeatedly until you arrive at a quotient less than 2. Arrange the remainder in the bottom-up direction as shown by the arrow.
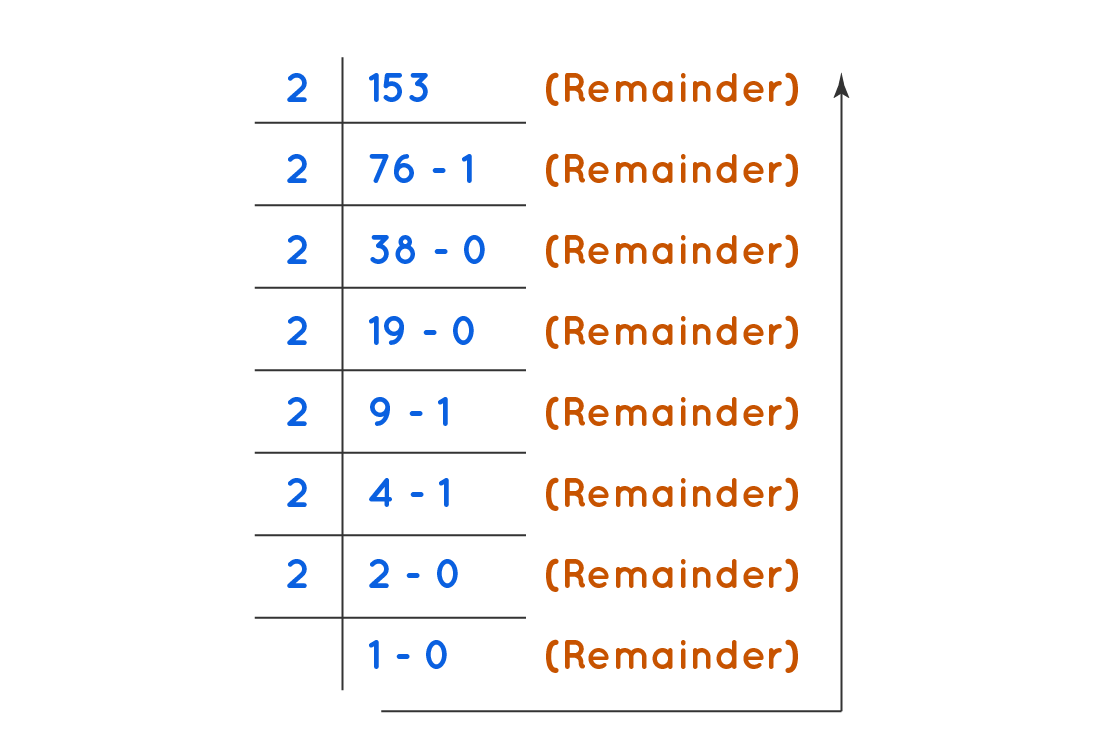
Therefore, \(153_{10}\) = \(10011001_{2}\) -
Example 2: Convert the hexadecimal number \(6BC_{16}\) to a base-10 decimal number.
Solution:Step 1: Get the decimal equivalent of the hexadecimal alphabet (B equals to 11 and C equals to 12)
Step 2: Multiply each digit with the power of 16 raised to its positional value.
Step 3: Add all the products.
\(6BC_{16}\) = (12 × 160) + (11 × 161) + (6 × 162)
= 12 + 176 + 1536
= \(1724_{10}\)
Therefore, \(6BC_{16}\) = \(1724_{10}\) -
Example 3: Convert \(163_{8}\) from base-8 (octal) to base-16 (hexadecimal) number system.
Solution:To solve this, we first convert the number from base-8 (octal) to base-10 (decimal) and then convert it from base-10 to base-16.
Step 1: Convert \(163_{8}\) to base-10
\(163_{8}\) = (3 × 80) + (6 × 81) + (1 × 82)
= 3+ 48+ 64
= \(115_{10}\)
Step 2: Now, let us convert \(115_{10}\) to base-16 (hexadecimal). To do this we divide 115 repeatedly by 16 until we get a quotient lesser than 16. This is shown below.

\(115_{10}\) = \(73_{16}\)
Therefore, \(163_{8}\) = \(73_{16}\) -
Example 4: Add the base-8 numbers \(161_{8}\) and \(264_{8}\).
Solution:Step 1: Convert both the base-8 numbers to base-10 numbers.
\(161_{8}\) = (1×80)+(6×81)+(1×82)
= 1+48+64
= \(113_{10}\)
\(264_{8}\) = (4×80)+(6×81)+(2×82)
= 4+48+128
= \(180_{10}\)
Step 2: Now add the base-10 numbers, \(113_{10}\) and \(180_{10}\), The result is 293.
Step 3: Now convert \(293_{10}\) to base-8 number.

\(293_{10}\) converts to \(445_{8}\). Therefore, \(161_{8}\) + \(264_{8}\) = \(445_{8}\).
FAQs on Base in Math
What are Number Systems?
A set of digits used to express and write numbers forms a number system.
Which is the Most Commonly Used Number System Around the World?
The decimal number system is the most commonly used number system around the world.
What is Meant by the Base of a Number System?
The total number of digits present in the number system is called the base of a number system.
What is the Number System that Computers Use?
Binary, decimal, octal, and hexadecimal are the number systems used by computers.
Can we Convert a Number in One Number System to Another?
Yes, we can convert a number in one number system to another.
What is Base-5 called?
A number system that uses 5 digits (0, 1, 2, 3, 4) to represent any number is called a base-5 number system. It is called the Quinary number system.
What is Base-8 called?
A number system that uses 8 numbers (0, 1, 2, 3, 4, 5, 6, 7) to express any number is called a base 8 number system. It is called the Octal number system.
visual curriculum
