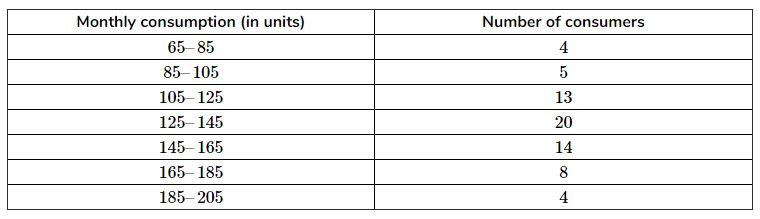
The following frequency distribution gives the monthly consumption of electricity of 68 consumers of a locality. Find the median, mean and mode of the data and compare them

Solution:

We will find the mean by step-deviation method

Mean, (x) = a + (Σfᵢuᵢ/Σfᵢ) × h

Modal Class is the class with the highest frequency

Mode = l + [(f₁ - f₀) / (2f₁ - f₀ - f₂)] × h

Here,

Class size, h

Lower limit of modal class, l

Frequency of modal class, f₁

Frequency of class preceding modal class, f₀

Frequency of class succeeding the modal class, f₂

Median Class is the class having Cumulative frequency(cf) just greater than n/2

Median = l + [(n/2 - cf)/f] × h

Class size, h

Number of observations, n

Lower limit of median class, l

Frequency of median class, f

Cumulative frequency of class preceding median class, cf

Class mark, xᵢ = (Upper class limit + Lower class limit)/2

Class size, h = 20

Taking assumed mean, a = 135

From the table, we obtain, Σfᵢ = 68 and Σfᵢuᵢ = 7

Mean, (x) = a + (Σfᵢuᵢ/Σfᵢ) × h

= 135 + (7/68) × 20

= 135 + 140/68

= 135 + 2.05

= 137.05

From the table, it can be observed that the maximum class frequency is 20, belonging to class interval 125 − 145.

Class size, h = 20

Modal class = 125 − 145

Lower limit of modal class, l = 125

Frequency of modal class, f₁ = 20

Frequency of class preceding modal class, f₀ = 13

Frequency of class succeeding the modal class, f₂ = 14

Mode = l + [(f₁ - f₀)/(2f₁ - f₀ - f₂)] × h

= 125 + [(20 - 13)/(2 × 20 - 13 - 14)] × 20

= 125 + [7/(40 - 27)] × 20

= 125 + (7/13) × 20

= 125 + 140/13

= 125 + 10.76

= 135.76

To find the median of the given data, cumulative frequency is calculated as follows:

From the table, we obtain

n = 68 ⇒ n/2 = 34

Cumulative frequency(cf) just greater than n/2 is 42, belonging to class-interval 125 − 145. Therefore, median class = 125 - 145

Therefore, median class = 125 - 145

Class size, h = 20

Lower limit of median class, l = 125

Frequency of median class, f = 20

Cumulative frequency of class preceding median class, cf = 22

Median = l + [(n/2 - cf)/f] × h

= 125 + [(34 - 22)/20] × 20

= 125 + 12

= 137

Therefore, median, mode, mean of the given data is 137, 135.76, and 137.05 respectively.

So, mean > median > mode

☛ Check: NCERT Solutions for Class 10 Maths Chapter 14

---

Video Solution:

The following frequency distribution gives the monthly consumption of electricity of 68 consumers of a locality. Find the median, mean and mode of the data and compare them.

NCERT Solutions for Class 10 Maths Chapter 14 Exercise 14.3 Question 1

Summary:

The median, mean and mode based on the frequency distribution data of the monthly consumption of electricity of 68 consumers of a locality are 137,135.76,and 137.05 respectively. So, mean > median > mode

---

☛ Related Questions:

• If the median of the distribution given below is 28.5, find the values of x and y.
• A life insurance agent found the following data for distribution of ages of 100 policy holders. Calculate the median age, if policies are given only to persons having age 18 years onwards but less than 60 year.
• The lengths of 40 leaves of a plant are measured correct to the nearest millimetre, and the data obtained is represented in the following table: Find the median length of the leaves. (Hint: The data needs to be converted to continuous classes for finding the median, since the formula assumes continuous classes. The classes then change to 117.5 - 126.5, 126.5 - 135.5, . . ., 171.5 - 180.5.).
• The following table gives the distribution of the life time of 400 neon lamps: Find the median lifetime of a lamp.