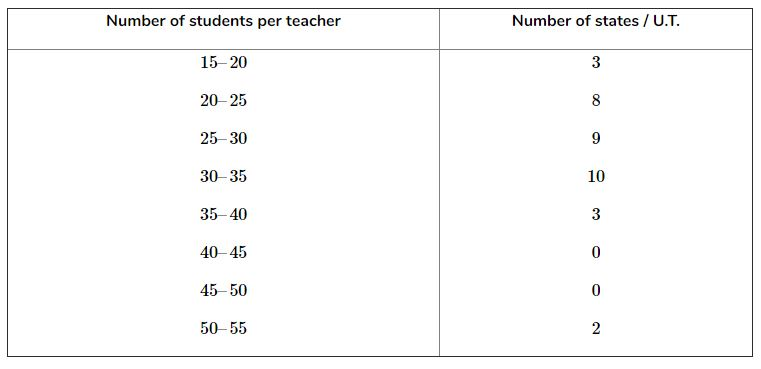
The following distribution gives the state-wise teacher-student ratio in higher secondary schools of India. Find the mode and mean of this data. Interpret the two measures.

Solution:

We will find the mean by direct method.

Mean, (x) = Σfᵢxᵢ/Σfᵢ

Modal Class is the class with the highest frequency

Mode = l + [(f₁ - f₀)/(2f₁ - f₀ - f₂)] × h

Here,

Class size, h

Lower limit of modal class, l

Frequency of modal class, f₁

Frequency of class preceding modal class, f₀

Frequency of class succeeding the modal class, f₂

To find mean, we know Class mark, xᵢ = (Upper class limit + Lower class limit)/2

Mean, (x) =  Σfᵢxᵢ/ Σfᵢ

= 1022.5/35

= 29.2

From the table, it can be observed that the maximum class frequency is 10, belonging to class interval 30 − 35

Therefore, modal class = 30 − 35

Class size, h = 5

Lower limit of modal class, l = 30

Frequency of modal class, f₁ = 10

Frequency of class preceding modal class, f₀ = 9

Frequency of class succeeding the modal class, f₂ = 3

Mode = l + (f₁ - f₀)/(2f₁ - f₀ - f₂) x h

= 30 + [(10 - 9)/(2 × 10 - 9 - 3)] × 5

= 30 + [1/(20 - 12)] × 5

= 30 + 5/8

= 30 + 0.625

= 30.625

≈ 30.6

The modal teacher-student ratio is 30.6 and mean teacher-student ratio is 29.2.

Most states / U.T. have a teacher-student ratio of 30.6 and on average the ratio is 29.2

☛ Check: NCERT Solutions for Class 10 Maths Chapter 14

---

Video Solution:

The following data gives the state-wise, teacher-student ratio in higher secondary schools of India. Find the mode and mean of the data and interpret the two measures

NCERT Solutions for Class 10 Maths Chapter 14 Exercise 14.2 Question 4

Summary:

The following data gives the state-wise, teacher-student ratio in higher secondary schools of India. The mode and mean of the data given are 30.6 and 29.2 respectively.

---

☛ Related Questions:

• The following table shows the ages of the patients admitted in a hospital during a year: Find the mode and the mean of the data given above. Compare and interpret the two measures of central tendency.
• The following data gives information on the observed lifetimes (in hours) of 225 electric components. Determine the modal lifetimes of the components.
• The following data gives the distribution of total monthly household expenditure of 200 families of a village. Find the modal monthly expenditure of the families. Also find the mean monthly expenditure.