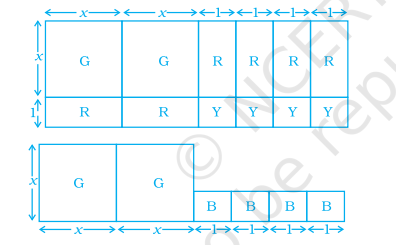
Take suitable number of cards given in the adjoining diagram [G(x × x) representing x², R (x × 1) representing x and Y (1 × 1) representing 1] to factorise the following expressions, by arranging the cards in the form of rectangles: (i) 2x² + 6x + 4 (ii) x² + 4x + 4. Factorise 2x² + 6x + 4 by using the figure.
Calculate the area of figure.
Solution:
Given, arrangement of cards in the form of algebraic expressions,
(i) 2x² + 6x + 4 (ii) x² + 4x + 4
Factorising these two expressions:
(i) 2x² + 6x + 4
Using the identity a² + 2ab + b² = (a + b)², the expression can be written as,
= 2x² + 4x + 2x + 4
= 2x(x + 2) + 2 (x + 2)
= (x + 2)(2x + 2) ← This is in the form of area of rectangle = length × breadth
= 2(x + 2) (x + 1)
(ii) x² + 4x + 4
Using the identity a² + 2ab + b² = (a + b)², the expression can be written as,
= x² + 2x + 2x + 4
= x(x + 2) + 2(x + 2)
= (x + 2) (x + 2) ← This is in the form of area of rectangle = length × breadth
= (x + 2)²
✦ Try This: Take suitable number of cards given in the adjoining diagram [G(x × x) representing x², R (x × 1) representing x and Y (1 × 1) representing 1] to factorise the expression, by arranging the cards in the form of rectangle: 2x² + 5x + 3. Calculate the area of figure.
☛ Also Check: NCERT Solutions for Class 8 Maths Chapter 9
NCERT Exemplar Class 8 Maths Chapter 7 Problem 123
Take suitable number of cards given in the adjoining diagram [G(x × x) representing x², R (x × 1) representing x and Y (1 × 1) representing 1] to factorise the following expressions, by arranging the cards in the form of rectangles: (i) 2x² + 6x + 4 (ii) x² + 4x + 4. Factorise 2x² + 6x + 4 by using the figure. Calculate the area of figure.

Summary:
Factorising the given arrangement of cards in the form of rectangles: (i) 2x² + 6x + 4 (ii) x² + 4x + 4, the area of the rectangles are 2(x + 2) (x + 1) and (x + 2)²
☛ Related Questions:
visual curriculum
