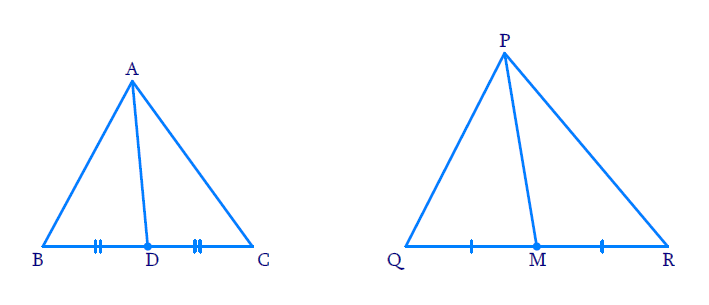
Sides AB and BC and median AD of a triangle ABC are respectively proportional to sides PQ and QR and median PM of ∆ PQR (see Fig. 6.41). Show that ∆ ABC ~ ∆ PQR

Solution:

We know that if one angle of a triangle is equal to one angle of the other triangle and the sides including these angles are proportional, then the two triangles are similar. This is referred to as SAS similarity criterion for two triangles.

In ΔABC and ΔPQR

AB/PQ = BC/QR = AD/PM [given]

AD and PM are median of ΔABC and ΔPQR respectively

⇒ BD/QM = (BC/2)/(QR/2) = BC/QR

Now, in ΔABD and ΔPQM

AB/PQ = BD/QM = AD/PM

⇒ ΔABD ∼ ΔPQM [SSS criterion]

Now, in ΔABC and ΔPQR

AB/PQ = BC/QR [given in the statement]

∠ABC = ∠PQR [∵ ΔABD ∼ ΔPQM]

⇒ ΔABC ∼ ΔPQR [SAS criteion]

☛ Check: NCERT Solutions Class 10 Maths Chapter 6

Video Solution:

Sides AB and BC and median AD of a triangle ABC are respectively proportional to sides PQ and QR and median PM of ∆ PQR (see Fig. 6.41). Show that ∆ ABC ~ ∆ PQR

NCERT Class 10 Maths Solutions Chapter 6 Exercise 6.3 Question 12

Summary:

In the above figure, sides AB and BC and median AD of a triangle ABC are respectively proportional to sides PQ, QR, and median PM of ∆PQR. Hence proved that ∆ABC ~ ∆ PQR.

☛ Related Questions:

• D is a point on the side BC of a triangle ABC such that ∠ADC = ∠ BAC. Show that CA^2 = CB.CD.
• Sides AB and AC and median AD of a triangle ABC are respectively proportional to sides PQ and PR and median PM of another triangle PQR. Show that ∆ABC ~ ∆ PQR.
• A vertical pole of length 6 m casts a shadow 4 m long on the ground and at the same time a tower casts a shadow 28 m long. Find the height of the tower
• If AD and PM are medians of triangles ABC and PQR, respectively where ΔABC ~ ΔPQR, prove that AB/PQ = AD/PM⋅