Prove that a diameter AB of a circle bisects all those chords which are parallel to the tangent at the point A
Solution:
Given, AB is the diameter of a circle.
AB bisects all those chords which are parallel to the tangent at the point A.
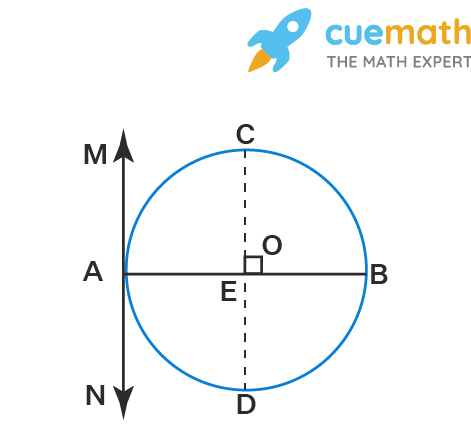
From the figure,
AB is the diameter of the circle.
CD is the chord of the circle.
MN is the tangent to the circle at the point A.
OA = OB = OC = OD = radius of the circle.
We know that the radius of a circle is perpendicular to the tangent at the point of contact.
So, OA ⟂ MN
Also, ∠MAO = ∠NAO = 90°
The corresponding angles are equal.
∠CEO = ∠MAO
So, ∠CEO = 90°
We know that the perpendicular drawn from the centre of the circle to the chord always bisects the chord.
It implies that OE bisects CD.
Therefore, diameter AB of a circle bisects all those chords which are parallel to the tangent at the point A.
✦ Try This: Prove that the diameter of a circle perpendicular to one of the two parallel chords of a circle is perpendicular to the other and bisects it.
☛ Also Check: NCERT Solutions for Class 10 Maths Chapter 10
NCERT Exemplar Class 10 Maths Exercise 9.3 Problem 10
Prove that a diameter AB of a circle bisects all those chords which are parallel to the tangent at the point A
Summary:
It is proven that a diameter AB of a circle bisects all those chords which are parallel to the tangent at the point A
☛ Related Questions:
- In Fig. 9.15, from an external point P, a tangent PT and a line segment PAB is drawn to a circle wit . . . .
- If a circle touches the side BC of a triangle ABC at P and extended sides AB and AC at Q and R, resp . . . .
- If a hexagon ABCDEF circumscribes a circle, prove that AB + CD + EF = BC + DE + FA
visual curriculum
