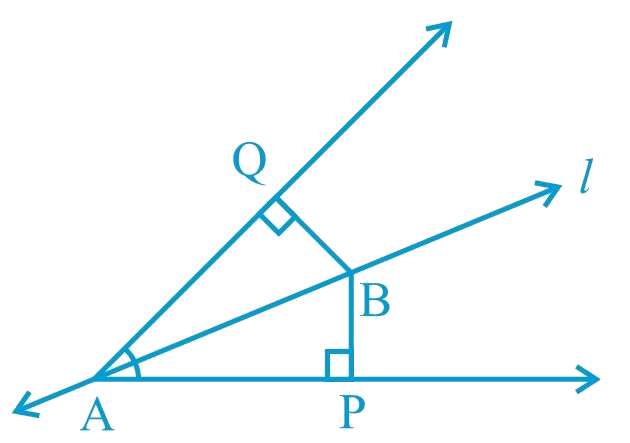
Line l is the bisector of an angle ∠A and B is any point on l. BP and BQ are perpendiculars from B to the arms of ∠A (see Fig. 7.20). Show that:
i) ΔAPB ≅ ΔAQB
ii) BP = BQ or B is equidistant from the arms of ∠A

Solution:

Given: l is the bisector of an angle ∠A and BP ⊥ AP and BQ ⊥ AQ

To Prove: ΔAPB ≅ ΔAQB and BP = BQ

i) We can show two triangles APB and AQB are congruent by using AAS congruency rule and then show that the corresponding parts of congruent triangles will be equal.

In ΔAPB and ΔAQB,

∠BAP = ∠BAQ (l is the angle bisector of ∠A)

∠APB = ∠AQB (Each 90°)

AB = AB (Common)

∴ ΔAPB ≅ ΔAQB (By AAS congruence rule)

ii) Since, ΔAPB ≅ ΔAQB

∴ BP = BQ (By CPCT)

Or, it can be said that point B is equidistant from the arms of ∠A.

☛ Check: NCERT Solutions Class 9 Maths Chapter 7

Video Solution:

Line l is the bisector of an angle ∠A and B is any point on l. BP and BQ are perpendiculars from B to the arms of ∠A (see Fig. 7.20). Show that: i) ΔAPB ≅ ΔAQB    ii) BP = BQ or B is equidistant from the arms of ∠A

NCERT Maths Solutions Class 9 Chapter 7 Exercise 7.1 Question 5

Summary:

If line L is the bisector of an angle ∠A and ∠B is any point on l, BP and BQ are perpendiculars from B the arms of ∠A, then ΔAPB ≅ ΔAQB using AAS congruence and BP = BQ or B is equidistant from the arms of ∠A using CPCT.

☛ Related Questions:

• In quadrilateral ACBD, AC = AD and AB bisects ∠A (See the given figure).Show that Δ ABC ≅ Δ ABD. What can you say about BC and BD?
• ABCD is a quadrilateral in which AD = BC and ∠DAB = ∠CBA (see the given figure). Prove thati) △ ABD ≅ △ BACii) BD = ACiii) ∠ABD = ∠BAC
• AD and BC are equal perpendiculars to a line segment AB (See the given figure). Show that CD bisects AB.
• l and m are two parallel lines intersected by another pair of parallel lines p and q. Show that ΔABC ≅ ΔCDA.