A day full of math games & activities. Find one near you.

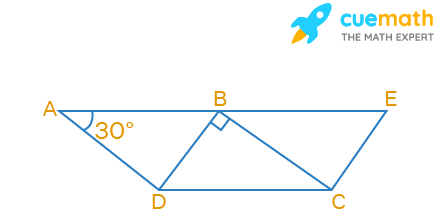
In the given figure, ABCD and BDCE are parallelograms with common base DC. If BC ⊥ BD, then ∠BEC =
(a) 60°
(b) 30°
(c) 150°
(d) 120°

Solution:

Given, ABCD and BDCE are parallelograms with common base DC.

BC ⊥ BD

We have to find the measure of ∠BEC.

From the figure,

∠BAD = 30°

We know that the opposite angles in a parallelogram are equal.

So, ∠BCD = 30°

Considering triangle CBD,

By angle sum property of a triangle, the sum of all three interior angles of a triangle is equal to 180 degrees.

We know that the opposite angles in a parallelogram are equal.

∠DBC + ∠BCD + ∠BDC = 180°

90° + 30° + ∠BDC = 180°

120° + ∠BDC = 180°

∠BDC = 180° - 120°

∠BDC = 60°

We know that the opposite angles in a parallelogram are equal.

So, ∠BEC = 60°

Therefore, the required angle is 60°.

✦ Try This: In a parallelogram, if one of the angle is 40°, then other three angles are

☛ Also Check: NCERT Solutions for Class 8 Maths

NCERT Exemplar Class 8 Maths Chapter 5 Problem 35

Summary:

In the given figure, ABCD and BDCE are parallelograms with common base DC. If BC ⊥ BD, then ∠BEC = 60°.

☛ Related Questions: