In the following figures, find the area of the shaded portions:

Solution:

 

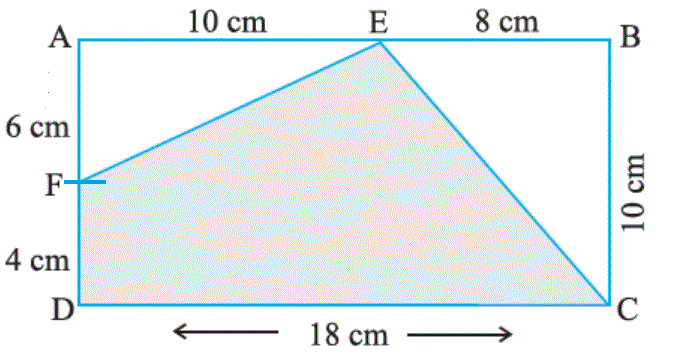
(i) Area of ∆ AEF = 1/2 × Base × Height

= 1/2 × 6 cm × 10 cm

= 30 cm²

Area of ∆ BCE = 1/2 × Base × Height

= 1/2 × 8 cm × 10 cm

= 40 cm²

Area of rectangle ABCD = Length × Breadth

= 18 cm × 10 cm

= 180 cm²

Area of shaded region = Area of rectangle ABCD - (Area of ∆ AEF + Area of ∆ BEC)

= 180 cm² - (30 cm² + 40 cm²)

= 180 cm² - 70 cm²

= 110 cm²

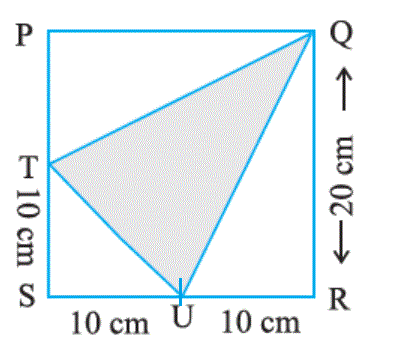
(ii) Area of ∆ PQT = 1/2 × Base × Height

= 1/2 × 20 cm × 10 cm

= 100 cm²

Area of ∆ QRU = 1/2 × Base × Height

= 1/2 × 10 cm × 20 cm

= 100 cm²

Area of ∆ STU = 1/2 × Base × Height

= 1/2 × 10 cm × 10 cm

= 50 cm²

Area of square PQRS = Side × Side

= 20 cm × 20 cm

= 400 cm²

Area of shaded region = Area of square PQRS - (Area of ∆ PQT + Area of ∆ QRU + Area of ∆ STU)

= 400 cm² - (100 cm² +100 cm² + 50 cm² )

= 400 cm² - 250 cm²

= 150 cm²

☛ Check: NCERT Solutions Class 7 Maths Chapter 11

---

Video Solution:

In the following figures, find the area of the shaded portion:

Maths NCERT Solutions Class 7 Chapter 11 Exercise 11.4 Question 10

Summary:

In the following figures, the area of the shaded portions is 110 cm² and 150 cm² respectively.

---

☛ Related Questions:

• Two Cross Roads Each Of Width 10 M Cut A Right Angles Through The Centre Of A Rectangular Park Of Length 700 M And Breadth 300 M And Parallel To Its Sides Find The Area Of The Roads
• Through A Rectangular Field Of Length 90 M And Breadth 60 M Two Roads Are Constructed Which Are Parallel To The Sides And Cut Each Other At Right Angles Through The Centre
• Pragya Wrapped A Cord Around A Circular Pipe Of Radius 4 Cm Adjoining Figure And Cut Off The Length Required Of The Cord Then She Wrapped It Around A Square Box Of Side 4 Cm
• The Adjoining Figure Represents A Rectangular Lawn With A Circular Flower Bed In The Middle Find I The Area Of The Whole Land Ii The Area Of The Flower Bed Iii The Area Of The Lawn