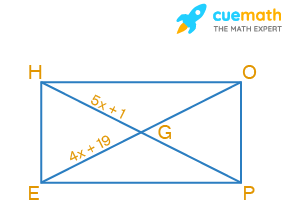
In the figure, HOPE is a rectangle. Its diagonals meet at G. If HG = 5x + 1 and EG = 4x + 19, find x
Solution:
Given, HOPE is a rectangle.
The diagonals HP and OE meet at G.
Given, HG = 5x + 1 and EG = 4x + 19
We have to find the value of x.
We know that the diagonals of a rectangle bisect each other.
So, HP = 2HG
HP = 2(5x + 1)
= 2(5x) + 2(1)
HP = 10x + 2
Similarly, OE = 2EG
OE = 2(4x + 19)
= 2(4x) + 2(19)
OE = 8x + 38
We know that the diagonals of a rectangle are equal.
So, HP = OE
10x + 2 = 8x + 38
10x - 8x = 38 - 2
2x = 36
x = 36/2
x = 18
Therefore, the required value of x is 18
✦ Try This: In the given figure, ABCD is a parallelogram. Find x.
☛ Also Check: NCERT Solutions for Class 8 Maths
NCERT Exemplar Class 8 Maths Chapter 5 Solved Problem 36
In the figure, HOPE is a rectangle. Its diagonals meet at G. If HG = 5x + 1 and EG = 4x + 19, find x
Summary:
In the figure, HOPE is a rectangle. Its diagonals meet at G. If HG = 5x + 1 and EG = 4x + 19, then x = 18.
☛ Related Questions: