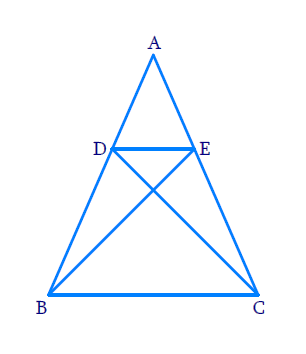
In Figure 6.37, if ∆ABE ≅ ∆ACD, show that ∆ADE ~ ∆ABC.

Solution:

We know that if two triangles are congruent to each other, their corresponding parts are equal.

If one angle of a triangle is equal to one angle of the other triangle and the sides including these angles are proportional, then the two triangles are similar.

This is referred to as SAS (Side - Angle - Side) similarity criterion for two triangles.

In ∆ABE and ∆ACD

AD = AE (∆ABE ≅ ∆ACD given).......... (1)

AB = AC (∆ABE ≅ ∆ACD given)......... (2)

Now Consider ∆ADE and ∆ABC

AD/AB = AE/AC [From equations (1) and (2)]

and ∠DAE = ∠BAC (Common angle)

Thus, ∆ADE ~ ∆ABC (SAS criterion)

☛ Check: Class 10 Maths NCERT Solutions Chapter 6

Video Solution:

In Figure 6.37, if ∆ABE ≅ ∆ACD, show that ∆ADE ~ ∆ABC.

NCERT Class 10 Maths Solutions Chapter 6 Exercise 6.3 Question 6

Summary:

In the above figure if ∆ABE ≅ ∆ACD, we have proved that ∆ADE ~ ∆ABC.

☛ Related Questions:

• In Fig. 6.38, altitudes AD and CE of Δ ABC intersect each other at the point P. Show that: (i) ΔAEP ~ ΔCDP (ii) ΔABD ~ ΔCBE (iii) ΔAEP ~ ΔADB (iv) ΔPDC ~ ΔBEC.
• E is a point on the side AD produced of a parallelogram ABCD and BE intersect CD at F. Show that ΔABE ~ ΔCFB.
• In Fig. 6.39, ABC and AMP are two right triangles, right angled at B and M respectively. Prove that: (i) ΔABC ~ ΔAMP (ii) CA/PA = BC/MP.
• CD and GH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ∆ABC and ∆EFG respectively. If ∆ABC ~ ∆FEG, show that: (i) CD/GH =AC/FG (ii) ∆DCB ~ ∆HGE (iii) ∆DCA ~ ∆HGF