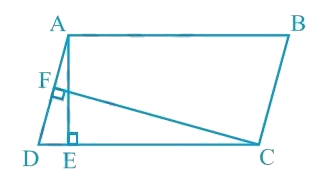
In Fig. 9.15, ABCD is a parallelogram, AE ⊥ DC and CF ⊥ AD. If AB = 16 cm, AE = 8 cm and CF = 10 cm, find AD.

Solution:

Given: AB = 16 cm, AE = 8 cm, CF = 10 cm

In parallelogram ABCD, CD = AB = 16 cm [Opposite sides of a parallelogram are equal]

We know that area of a parallelogram = Base × Corresponding altitude

Therefore, Area of a parallelogram ABCD = CD × AE = AD × CF

Here CD and AD act as the base and AE ⊥ CD, CF ⊥ AD are the corresponding altitudes.

∴ AD = (CD × AE) / CF

Substituting the values for CD, AE, and CF, we get AD = (16 × 8) /10 cm = 12.8 cm

Thus, the length of AD is 12.8 cm.

☛ Check: NCERT Solutions for Class 9 Maths Chapter 9

Video Solution:

In Fig. 9.15, ABCD is parallelogram, AE ⊥ DC and CF ⊥ AD. If AB = 16 cm, AE = 8 cm and CF = 10 cm, find AD.

NCERT Maths Solutions Class 9 Chapter 9 Exercise 9.2 Question 1

Summary:

If ABCD is parallelogram AE ⊥ DC, CF ⊥ AD, and AB = 16cm, AE = 8cm, CF = 10cm, then the value of AD is 12.8cm in the given figure.

☛ Related Questions:

• If E, F, G, and H are respectively the mid-points of the sides of a parallelogram ABCD, show that ar (EFGH) = 1/2 ar (ABCD).
• P and Q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD. Show that ar (APB) = ar (BQC).
• In Fig. 9.16, P is a point in the interior of a parallelogram ABCD. Show that (i) ar (APB) + ar (PCD) = 1/2 ar (ABCD) (ii) ar (APD) + ar (PBC) = ar (APB) + ar (PCD) [Hint: Through P, draw a line parallel to AB.]
• In Fig. 9.17, PQRS and ABRS are parallelograms and X is any point on side BR. Show that (i) ar (PQRS) = ar (ABRS) (ii) ar (AXS) = 1/2 ar (PQRS)