In Fig 7.51, PR > PQ and PS bisects ∠QPR. Prove that ∠PSR > ∠PSQ.

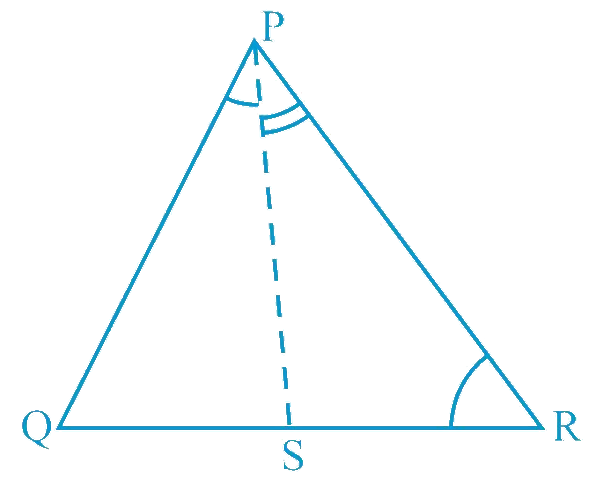
Solution:

Given: PR > PQ and PS bisects ∠QPR

To prove: ∠PSR > ∠PSQ

As PR > PQ, ∠PQS > ∠PRS (Angle opposite to larger side is larger ) ...(1)

PS is the angle bisector of ∠QPR.

∠QPS = ∠RPS ...(2) [Since,PS bisects ∠QPR]

∠PSR is the exterior angle of ΔPQS.

∠PSR = ∠PQS + ∠QPS ...(3) [Using  exterior angle sum property]

∠PSQ is the exterior angle of ΔPRS.

∠PSQ = ∠PRS + ∠RPS ...(4) [Using exterior angle sum property]

From Equations (1) and (2), we obtain

∠PQS + ∠QPS > ∠PRS + ∠RPS

∠PSR > ∠PSQ [From Equations (3) and (4)]

☛ Check: NCERT Solutions Class 9 Maths Chapter 7

Video Solution:

In Fig 7.51, PR > PQ and PS bisects ∠QPR. Prove that ∠PSR > ∠PSQ.

NCERT Maths Solutions Class 9 Chapter 7 Exercise 7.4 Question 5

Summary:

If in the given figure, PR > PQ and PS bisects ∠QPR, we have proved that ∠PSR > ∠PSQ.

☛ Related Questions:

• Show that in a right-angled triangle, the hypotenuse is the longest side.
• In Fig. 7.48, sides AB and AC of Δ ABC are extended to points P and Q respectively. Also, ∠PBC < ∠QCB. Show that AC > AB.
• In the given figure, ∠B < ∠A and ∠C < ∠D. Show that AD < BC.
• AB and CD are respectively the smallest and longest sides of a quadrilateral ABCD (see Fig. 7.50). Show that ∠A > ∠C and ∠B > ∠D.