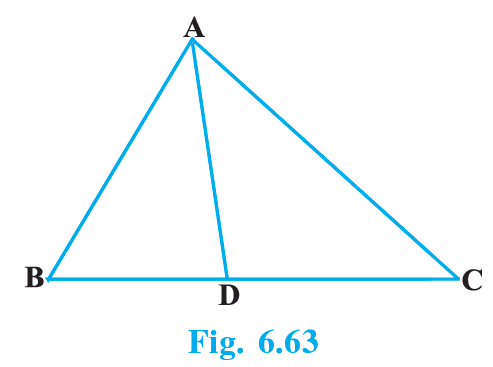
In Fig. 6.63, D is a point on side BC of ∆ABC such that BD/CD = AB/AC. Prove that AD is the bisector of ∠BAC

Solution:

Let's extend BA to E such that AE = AC and join CE.

In ∆AEC

AE = AC

⇒ ∠ACE = ∠AEC ......(i) [Angles opposite to equal sides are equal]

It is given that

BD/CD = BA/CA

BD/CD = BA/AE [Since, AC = AE] .......(ii)

In ∆ABD and ∆EBC

AD || EC (Converse of Basic Proportionality Theorem)

⇒ ∠BAD = ∠BEC (Corresponding angles) .......(iii)

and ∠DAC = ∠ACE (Alternate interior angles) .......(iv)

or ∠DAC = ∠AEC [From (i) and (iv)] ......... (v)

From (iii) and (v),

∠BAD = ∠DAC

Thus, AD is the bisector of ∠BAC

☛ Check: NCERT Solutions for Class 10 Maths Chapter 6

Video Solution:

In Fig. 6.63, D is a point on side BC of ∆ABC such that BD/CD = BA/CA. Prove that: AD is the bisector of ∠BAC

NCERT Class 10 Maths Solutions Chapter 6 Exercise 6.6 Question 9

Summary:

In the above figure, D is a point on side BC of ∆ABC such that BD/CD = BA/CA. Hence proved that AD is the bisector of ∠BAC.

☛ Related Questions:

• In Fig. 6.56, PS is the bisector of ∠QPR of ΔPQR. Prove that QS/SR = PQ/PR.
• In Fig. 6.57, D is a point on hypotenuse AC of ΔABC , such that BD ⊥ AC, DM ⊥ BC and DN ⊥ AB. Prove that: (i) DM² = DN.MC (ii) DN² = DM.AN.
• In Fig. 6.58, ABC is a triangle in which ∠ABC > 90° and AD ⊥ CB produced. Prove that: AC² = AB² + BC² + 2BC.BD.
• In Fig. 6.59, ABC is a triangle in which ∠ABC less than 90° and AD ⊥ BC. Prove that: AC² = AB² + BC² - 2BC × BD.