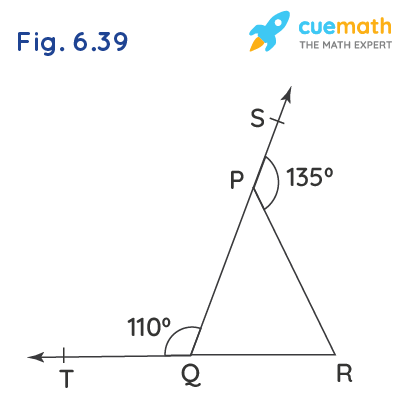
In Fig. 6.39, sides QP and RQ of ∆PQR are produced to points S and T respectively. If ∠SPR = 135° and ∠PQT = 110°, find ∠PRQ.
Solution:
Given: ∠SPR = 135° and ∠PQT = 110°
To find: ∠PRQ
We know that if non-common arms of two adjacent angles form a line, then these angles are called linear pair angle and their sum is equal to 180°.
If the sum of two adjacent angles is 180° then the two non-common arms of the angles form a line.
According to Angle sum property of a triangle , sum of the interior angles of a triangle is 180°.
∠SPR + ∠QPR = 180° [Linear pair]
135° + ∠QPR = 180°
∠QPR = 180° - 135°
∠QPR = 45°.....(i)
∠PQT + ∠PQR = 180° [Linear pair]
110° + ∠PQR = 180°
∠PQR = 180° - 110°
∠PQR = 70°.....(ii)
Now,
∠PQR + ∠QPR + ∠PRQ = 180° [Angle sum property of a triangle]
70°+ 45° + ∠PRQ = 180° [from (i) and (ii)]
∠PRQ = 180° - 115°
∠PRQ = 65°
☛ Check: NCERT Solutions Class 9 Maths Chapter 6
Video Solution:
In Fig. 6.39, sides QP and RQ of ∆PQR are produced to points S and T respectively. If ∠SPR = 135° and ∠PQT = 110°, find ∠PRQ.
NCERT Maths Solutions Class 9 Chapter 6 Exercise 6.3 Question 1
Summary:
In Fig. 6.39, sides QP and RQ of ΔPQR are produced to points S and T respectively, if ∠SPR = 135° and ∠PQT = 110°, then the value of ∠PRQ = 65°.
☛ Related Questions:
- In Fig. 6.40, ∠X = 62°, ∠XYZ = 54°. If YO and ZO are the bisectors of ∠XYZ and ∠XZY respectively of ∠XYZ, find ∠OZY and ∠YOZ.
- In Fig. 6.41, if AB || DE, ∠BAC = 35° and ∠CDE = 53°, find ∠DCE.
- In Fig. 6.42, if lines PQ and RS intersect at point T, such that ∠PRT = 40°, ∠RPT = 95° and ∠TSQ = 75°, find ∠SQT.
- In Fig. 6.43, if PQ ⊥ PS, PQ || SR, ∠SQR = 28° and ∠QRT = 65° then find the values of x and y.
visual curriculum