In Fig. 6.16, if x + y = w + z, then prove that AOB is a line.
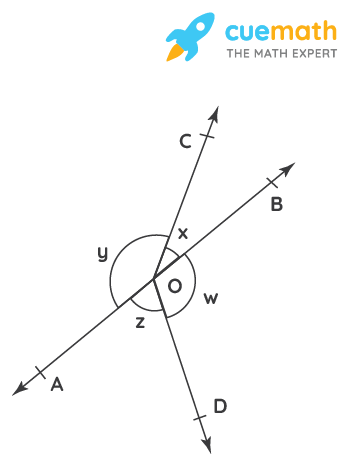
Solution:
Given: x + y = w + z
To prove: AOB is a line.
We know that if the sum of two adjacent angles is 180°, then the non-common arms of the angles form a line.

From the figure we can see that,
(x + y) + (w + z) = 360° (complete angle)
It is given that (x + y) = (w + z),
Hence (x + y) + (w + z) = 360° can be written as (x + y) + (x + y) = 360°
2x + 2y = 360°
2(x + y) = 360°
x + y = 360°/2 = 180°
Since the sum of adjacent angles, x and y with OA and OB as the non-common arms is 180° we can say that AOB is a line.
☛ Check: NCERT Solutions Class 9 Maths Chapter 6
Video Solution:
In Fig. 6.16, if x + y = w + z, then prove that AOB is a line.
NCERT Solutions Class 9 Maths Chapter 6 Exercise 6.1 Question 4
Summary:
In Fig. 6.16, given that x + y = w + z, thus we have proved that AOB is a line as the sum of adjacent angles, x and y with OA and OB as the non-common arms is 180°.
☛ Related Questions:
- In Fig. 6.28, find the values of x and y and then show that AB||CD.
- In Fig. 6.30, if AB||CD, EF ⊥ CD and ∠GED =126°, find ∠AGE, ∠GEF and ∠FGE.
- In Fig. 6.31, if PQ || ST, ∠PQR = 110° and ∠RST = 130°, find ∠QRS.[Hint: Draw a line parallel to ST through point R.]
- In Fig. 6.32, if AB || CD, ∠APQ = 50° and ∠PRD = 127°, find x and y.
visual curriculum
