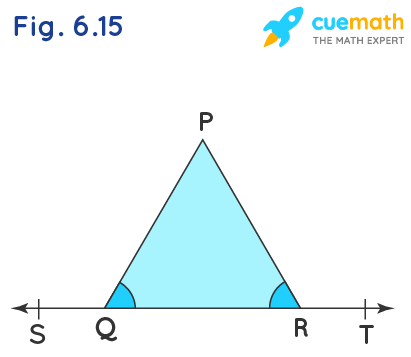
In Fig. 6.15, ∠PQR = ∠PRQ, then prove that ∠PQS = ∠PRT.

Solution:

Given: ∠PQR = ∠PRQ

To prove: ∠PQS = ∠PRT

We know that, if a ray stands on a line, then the sum of adjacent angles formed is 180°.

Let ∠PQR = ∠PRQ = a.

Let ∠PQS = b and ∠PRT = c.

Lines ST and PQ intersect at point Q, hence the sum of adjacent angles ∠PQS and ∠PQR is 180°.

∠PQS + ∠PQR = 180°

b + a = 180°

b = 180° - a….(1)

Lines ST and PR intersect at point R, hence the sum of adjacent angles ∠PRQ and ∠PRT is 180°.

∠PRQ + ∠PRT = 180°

a +  c  = 180°

c = 180° - a ….(2)

From equations (1) and (2), it is clear that b = c. Hence ∠PQS = ∠PRT is proved.

☛ Check: NCERT Solutions Class 9 Maths Chapter 6

Video Solution:

In Fig. 6.15, ∠PQR = ∠PRQ then prove that ∠PQS = ∠PRT.

NCERT Solutions Class 9 Maths Chapter 6 Exercise 6.1 Question 3

Summary:

In Fig. 6.15, given that ∠PQR = ∠PRQ, hence we have proved that ∠PQS = ∠PRT.

☛ Related Questions:

• In Fig. 6.13, lines AB and CD intersect at O. If ∠AOC + ∠BOE = 70° and ∠BOD = 40°, find ∠BOE and reflex ∠COE.
• In Fig. 6.14, lines XY and MN intersect at O. If ∠POY = 90° and a : b = 2 : 3, find c.
• In Fig. 6.16, if x + y = w + z, then prove that AOB is a line.
• In Fig. 6.17, POQ is a line. Ray OR, is perpendicular to line PQ. OS another ray lying between rays OP and OR. Prove that ∠ROS = 1/2 (∠QOS - ∠POS).