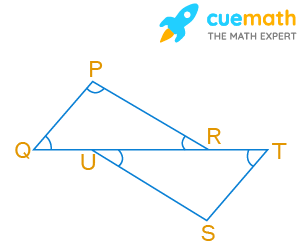
In Fig. 6.41, ∆PQR is right-angled at P. U and T are the points on line QRF. If QP || ST and US || RP, find ∠S.

Solution:

Given, PQR is a triangle right-angled at P.

U and T are the points on the line QRF.

Also, QP || ST and US || RP

We have to find the measure of ∠S.

If two parallel lines are cut by a transversal, then each pair of alternate interior angles are equal.

Considering QP || ST with QT as transversal,

The alternate interior angles are PQR and STU

So, ∠PQR = ∠STU

Considering DS || RP with QT as transversal,

The alternate interior angles are PQR and STU

So, ∠PRQ = ∠SUT

We observe that two angles of the triangle PQR and STU are equal, so the third angle will also be equal.

Angle-Angle-Angle congruence rule states that if three sides of one triangle are equal to three corresponding sides of another triangle, then the triangles are congruent.

By AAA rule, ∆PQR ≅ ∆STU

So, ∠RPQ = ∠UST

Since ∠P = 90°, the value of ∠S = 90°

Therefore, the value of angle S is 90 degrees.

✦ Try This: In ΔPQR and ΔMST, ∠P = 55°, ∠Q =25°, ∠M = 100° and ∠S = 25°. Is ΔQPR ~ ΔTSM? Why?

☛ Also Check: NCERT Solutions for Class 7 Maths Chapter 6

NCERT Exemplar Class 7 Maths Chapter 6 Problem 133

In Fig. 6.41, ∆PQR is right-angled at P. U and T are the points on line QRF. If QP || ST and US || RP, find ∠S.

Summary:

In Fig. 6.41, ∆PQR is right-angled at P. U and T are the points on line QRF. If QP || ST and US || RP, ∠S is 90°.

☛ Related Questions:

• In each of the given pairs of triangles of Fig. 6.42, applying only ASA congruence criterion, determ . . . .
• In each of the given pairs of triangles of Fig. 6.43 ABCD, using only RHS congruence criterion, dete . . . .
• In each of the given pairs of triangles of Fig. 6.43 UXYZ, using only RHS congruence criterion, dete . . . .