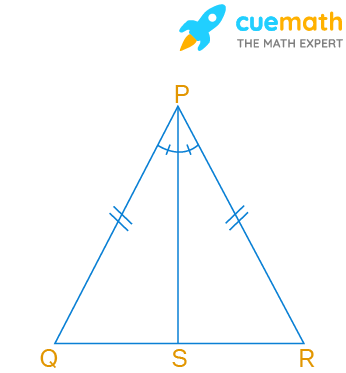
In Fig. 6.3, PS is the bisector of ∠P and PQ = PR. Then ∆PRS and ∆PQS are congruent by the criterion
a. AAA
b. SAS
c. ASA
d. both b. and c
Solution:
Given, PS is the bisector of ∠P
Also, PQ = PR
We have to determine by which criterion ∆PRS and ∆PQS are congruent.
(i) AAA - Angle-Angle-Angle congruence rule
Angle-Angle-Angle congruence rule states that if three sides of one triangle are equal to three corresponding sides of another triangle, then the triangles are congruent.
Therefore, option a does not satisfy the given conditions.
(ii) SAS - Side-Angle-Side congruence rule
The SAS criterion states that If two sides of one triangle are respectively proportional to two corresponding sides of another, and if the included angles are equal, then the two triangles are congruent.
Therefore, option b satisfies the given conditions.
(iii) ASA - Angle-Side-Angle congruence rule
ASA congruence criterion states that, "if two angles of one triangle, and the side contained between these two angles, are respectively equal to two angles of another triangle and the side contained between them, then the two triangles will be congruent".
Therefore, option c does not satisfy the given conditions.
✦ Try This: Can 2.2 cm, 3.3 cm and 4.4 cm form the sides of a triangle? Justify your answer
☛ Also Check: NCERT Solutions for Class 7 Maths Chapter 6
NCERT Exemplar Class 7 Maths Chapter 6 Sample Problem 5
In Fig. 6.3, PS is the bisector of ∠P and PQ = PR. Then ∆PRS and ∆PQS are congruent by the criterion, a. AAA, b. SAS, c. ASA, d. both b. and c
Summary:
In Fig. 6.3, PS is the bisector of ∠P and PQ = PR. Then ∆PRS and ∆PQS are congruent by the criterion SAS
☛ Related Questions:
- The line segment joining a vertex of a triangle to the mid-point of its opposite side is called its . . . .
- A triangle is said to be ________, if each one of its sides has the same length. Fill in the blanks . . . .
- In Fig. 6.4, ∠PRS = ∠QPR + ∠ ________ . Fill in the blanks to make the statement true.
visual curriculum