A day full of math games & activities. Find one near you.

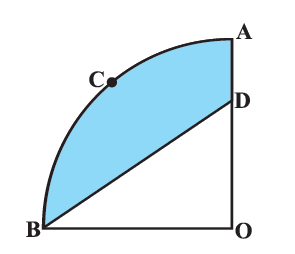
In Fig. 12.30, OACB is a quadrant of a circle with centre O and radius 3.5 cm. If OD = 2 cm, find the area of the
(i) quadrant OACB, (ii) shaded region

Solution:

We use the formula for area of sector of the circle to solve the problem.

Since quadrant means 1/4^th of a complete circle, therefore, the angle at the centre of a quadrant of a circle, θ = 360°/4 = 90°

Area of the quadrant OACB = 1/4πr²

We can get the area of quadrant OACB with radius r = 3.5 cm

Area of shaded region = Area of quadrant OACB - Area of ΔBDO

Since ∠BOD = 90°, ΔBDO is a right-angled triangle.

Using formula, Area of triangle = 1/2 × base × height , we can find area of ΔBDO with base = OB = 3.5 cm (radius of quadrant) and height = OD = 2 cm

(i) Area of quadrant OACB = 1/4πr²

= 1/4 × 22/7 × (3.5 cm)²

= 1/4 × 22/7 × 7/2 × 7/2 cm²

= 77/8 cm²

(ii) In ΔBDO, OB = r = 3.5 cm = 7/2 cm and OD = 2 cm

Area of ΔBDO = 1/2 × base × height

= 1/2 × OB × OD

= 1/2 × 7/2 cm × 2 cm

= 7/2 cm²

From figure, it is observed that:

Area of shaded region = Area of Quadrant OACB - Area of ΔBDO

= 77/8 cm² - 7/2 cm²

= (77 - 28)/8 cm²

= 49/8 cm²

☛ Check: NCERT Solutions Class 10 Maths Chapter 12

Video Solution:

NCERT Solutions Class 10 Maths Chapter 12 Exercise 12.3 Question 12

Summary:

The area of the quadrant OACB of a circle with center O and radius 3.5 cm and the area of the shaded region are 77/8 cm² and 49/8 cm² respectively.

☛ Related Questions: