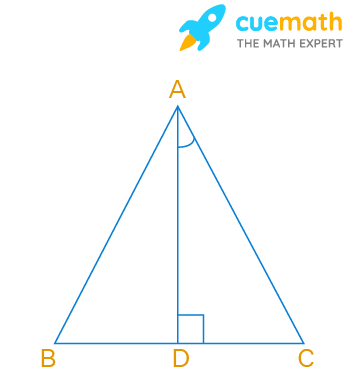
In an equilateral triangle ABC (Fig. 6.2), AD is an altitude. Then 4AD² is equal to
a. 2BD²
b. BC²
c. 3AB²
d. 2DC²

Solution:

Given, ABC is an equilateral triangle with AD as altitude.

We have to find the value of 4AD².

We know that in an equilateral triangle all the sides are of equal length.

Let AB = BC = AC = x units --------- (1)

Let AD = h units ---------------------- (2)

In an equilateral triangle, the altitude AD bisects BC

So, BD = CD = BC/2 = x/2

Considering triangle ADB,

We observe that ADB is a right angle triangle with D equal to 90 degrees.

AD² + BD² = AB²

(h)² + (x/2)² = (x)²

h² + x²/4 = x²

h² = x² - x²/4

h² = [(4-1)/4]x²

h² = (3/4)x²

4h² = 3x²

From (1) and (2),

4AD² = 3AB² = 3BC² = 3AC²

Therefore, 4AD² = 3AB²

✦ Try This: In ∆PQR, ∠P = 70°, ∠Q = 65 ° then find ∠R

☛ Also Check: NCERT Solutions for Class 7 Maths Chapter 6

NCERT Exemplar Class 7 Maths Chapter 6 Sample Problem 2

In an equilateral triangle ABC (Fig. 6.2), AD is an altitude. Then 4AD² is equal to, a. 2BD², b. BC², c. 3AB², d. 2DC²

Summary:

In an equilateral triangle ABC (Fig. 6.2), AD is an altitude. Then 4AD² is equal to 3AB²

☛ Related Questions: