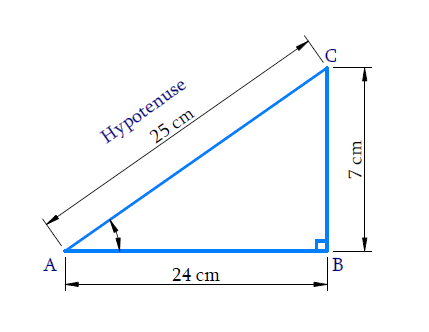
In ∆ ABC, right-angled at B, AB = 24 cm, BC = 7 cm. Determine :
(i) sin A, cos A   (ii) sin C, cos C

Solution:

We use the basic formulas of trigonometric ratios to solve the question.

Applying the Pythagoras theorem for ∆ABC, we can find the hypotenuse (side AC). Once hypotenuse is known, we can find sine and cosine angles using trigonometric ratios.

In ΔABC, we obtain,

AC² = AB² + BC²

= 24²  + 7²

= 576 + 49

= 625 

∴ Hypotenuse AC = √625 cm = 25 cm

(i)

sin A = side opposite to ∠A / hypotenuse = BC/AC

sin A = 7 cm /25 cm = 7/25

sin A = 7/25

cos A = side adjacent to ∠A / hypotenuse = AB/AC

= 24 cm / 25 cm = 24/25

cos A = 24/25

(ii)

sin C = side opposite to ∠C / hypotenuse = AB/AC

sin C = 24 cm / 25 cm = 24/25

sin C = 24/25

cos C = side adjacent to ∠C / hypotenuse = BC/AC

= 7 cm / 25 cm = 7/25

cos C = 7/25

☛ Check: NCERT Solutions Class 10 Maths Chapter 8

---

Video Solution:

In ΔABC, right-angled at B, AB = 24 cm, BC = 7 cm. Determine: (i) sin A, cos A (ii) sin C, cos C

Maths NCERT Solutions Class 10 Chapter 8 Exercise 8.1 Question 1

Summary:

In ΔABC, right-angled at B, AB = 24 cm, BC = 7 cm, then sin A, cos A is 7/25 and 24/25 respectively and sin C, cos C is 24/25 and 7/25 respectively.

---

☛ Related Questions:

• In Fig. 8.13, find tan P – cot R.
• If sin A = 3/4 calculate cos A and tan A.
• Given 15 cot A = 8, find sin A and sec A.
• Given sec θ = 13/12, calculate all other trigonometric ratios.