A day full of math games & activities. Find one near you.

If x̄1, x̄2, x̄3, ….., x̄n are the means of n groups with n1 , n2 , ... , nn number of observations respectively, then the mean x̄ of all the groups taken together is given by :

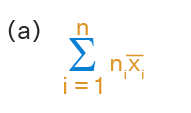
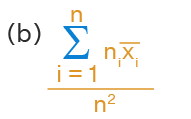
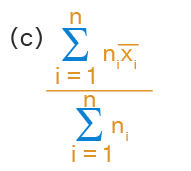
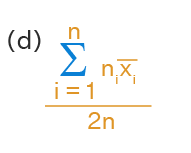
Solution:

It is given that

The mean of n groups is x̄1, x̄2, x̄3, ….., x̄n having n1, n2, ….. nn number of observations

\(n_{1}\overline{x_{1}}=\sum_{i=1}^{n_{1}}x_{i}\), \(n_{2}\overline{x_{2}}=\sum_{j=1}^{n_{2}}x_{j}\), \(n_{3}\overline{x_{3}}=\sum_{k=1}^{n_{3}}x_{k}\), …… \(n_{n}\overline{x_{n}}=\sum_{p=1}^{n_{n}}x_{p}\)

We can write the mean of all groups x̄ as

\(\\\overline{x}=\frac{\sum_{i=1}^{n_{1}}x_{i}+\sum_{j=1}^{n_{2}}x_{j}+\sum_{k=1}^{n_{3}}x_{k}+....+\sum_{p=1}^{n_{n}}x_{p}}{n_{1}+n_{2}+....+n_{n}}\\\\\overline{x}= \frac{n_{1}\overline{x_{1}}+n_{2}\overline{x_{2}}+n_{3}\overline{x_{3}}+...+n_{n}\overline{x_{n}}}{n_{1}+n_{2}+....+n_{n}}\\\overline{x}=\frac{\sum_{i=1}^{n}n_{i}\overline{x_{i}}}{\sum_{i=1}^{n}n_{i}} \)

Therefore, the mean x̄ of all the groups taken together is given by \(\overline{x}=\frac{\sum_{i=1}^{n}n_{i}\overline{x_{i}}}{\sum_{i=1}^{n}n_{i}} \).

✦ Try This: The mean of five numbers is 24. If one number is excluded, their mean becomes 20. The excluded number is :

☛ Also Check: NCERT Solutions for Class 9 Maths Chapter 14

NCERT Exemplar Class 9 Maths Exercise 14.1 Problem 17

If x̄1, x̄2, x̄3, ….., x̄n are the means of n groups with n1 , n2 , ... , nn number of observations respectively, then the mean x̄ of all the groups taken together is given by

Summary:

If x̄1, x̄2, x̄3, ….., x̄n are the means of n groups with n1 , n2 , ... , nn number of observations respectively, then the mean x̄ of all the groups taken together is given by

☛ Related Questions: