If bisectors of opposite angles of a cyclic quadrilateral ABCD intersect the circle, circumscribing it at the points P and Q, prove that PQ is a diameter of the circle.
Solution:
Given, ABCD is a cyclic quadrilateral
The bisectors of opposite angles of a cyclic quadrilateral ABCD intersect the circle, circumscribing it at the points P and Q.
We have to prove that PQ is a diameter of the circle.
Join QD and QC.
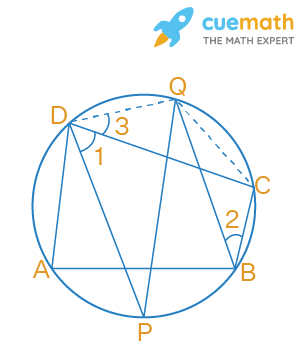
We know that the sum of opposite angles of a cyclic quadrilateral is equal to 180 degrees.
∠CDA + ∠CBA = 180°
Dividing by 2 on both sides,
1/2 ∠CDA + 1/2 ∠CBA = 1/2 (180°)
Given, the bisectors of opposite angles of a cyclic quadrilateral ABCD intersect the circle
∠1 = 1/2 ∠CDA
∠2 = 1/2 ∠CBA
So, ∠1 + ∠2 = 90° --------------------------- (1)
We know that the angles in the same segment of a circle are equal.
Considering segment QC,
∠2 = ∠3 --------------------------------------- (2)
From (1) and (2),
∠1 + ∠3 = 90°
∠PDQ = 90°
We know that the diameter of the circle subtends a right angle at the circumference
Therefore, PQ is the diameter of a circle.
✦ Try This: If the sector of a circle of diameter 10 cm subtends an angle of 144° at the centre, then the length of the arc of the sector is equal to?
☛ Also Check: NCERT Solutions for Class 9 Maths Chapter 10
NCERT Exemplar Class 9 Maths Exercise 10.4 Problem 9
If bisectors of opposite angles of a cyclic quadrilateral ABCD intersect the circle, circumscribing it at the points P and Q, prove that PQ is a diameter of the circle.
Summary:
If bisectors of opposite angles of a cyclic quadrilateral ABCD intersect the circle, circumscribing it at the points P and Q, it is proven that PQ is a diameter of the circle
☛ Related Questions:
- A circle has a radius √2 cm. It is divided into two segments by a chord of length 2 cm. Prove that t . . . .
- Two equal chords AB and CD of a circle when produced intersect at a point P. Prove that PB = PD
- AB and AC are two chords of a circle of radius r such that AB = 2AC. If p and q are the distances of . . . .
visual curriculum
