For each of the following numbers, find the smallest whole number by which it should be multiplied so as to get a perfect square number. Also find the square root of the square number so obtained.
(i) 252 (ii) 180 (iii) 1008 (iv) 2028 (v) 1458 (vi) 768

Solution:

We have to find the smallest whole number by which the number should be multiplied so as to get a perfect square number

To get a perfect square, each factor of the given number must be paired.

(i) 252

Hence, prime factor 7 does not have its pair. If 7 gets a pair, then the number becomes a perfect square. Therefore, 252 has to be multiplied by 7 to get a perfect square.

So, perfect square is 252 × 7 = 1764

1764 = 2 × 2 × 3 × 3 × 7 × 7

Thus, √1764 = 2 × 3 × 7 = 42

(ii) 180

Hence, prime factor 5 does not have its pair. If 5 gets a pair, then the number becomes a perfect square. Therefore, 180 has to be multiplied by 5 to get a perfect square.

So, perfect square is 180 × 5 = 900

900 = 2 × 2 × 3 × 3 × 5 × 5

Thus, √900 = 2 × 3 × 5 = 30

(iii) 1008

Hence, prime factor 7 does not have its pair. If 7 gets a pair, then the number becomes a perfect square. Therefore, 1008 has to be multiplied by 7 to get a perfect square.

So, perfect square is 1008 × 7 = 7056

7056 = 2 × 2 × 2 × 2 × 3 × 3 × 7 × 7

Thus, √7056 = 2 × 2 × 3 × 7 = 84

(iv) 2028

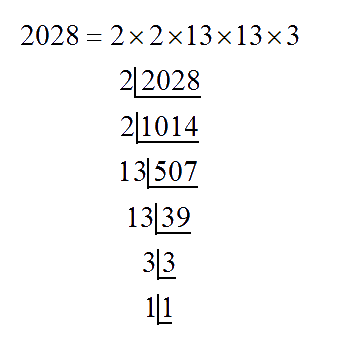
Hence, prime factor 3 does not have its pair. If 3 gets a pair, then the number becomes a perfect square. Therefore, 2028 has to be multiplied by 3 to get a perfect square.

So, perfect square is 2028 × 3 = 6084

6084 = 2 × 2 × 13 × 13 × 3 × 3

Thus, √6084 = 2 × 13 × 3 = 78

(v) 1458

Hence, prime factor 2 does not have its pair. If 2 gets a pair, then the number becomes a perfect square. Therefore, 1458 has to be multiplied by 2 to get a perfect square.

So, perfect square is 1458 × 2 = 2916

2916 = 3 × 3 × 3 × 3 × 3 × 3 × 2 × 2

Thus, √2916 = 3 × 3 × 3 × 2 = 54

(vi) 768

Hence, prime factor 3 does not have its pair. If 3 gets a pair, then the number becomes a perfect square. Therefore, 768 has to be multiplied by 3 to get a perfect square.

So, perfect square is 768 × 3 = 2304

2304 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 3 × 3

Thus, √2304 = 2 × 2 × 2 × 2 × 3 = 48

☛ Check: NCERT Solutions for Class 8 Maths Chapter 6

---

Video Solution:

For each of the following numbers, find the smallest whole number by which it should be multiplied so as to get a perfect square number. Also find the square root of the square number so obtained.
(i) 252 (ii) 180 (iii) 1008 (iv) 2028 (v) 1458 (vi) 768

NCERT Solutions for Class 8 Maths Chapter 6 Exercise 6.3 Question 5

Summary:

For each of the following numbers, (i) 252 (ii) 180 (iii) 1008 (iv) 2028 (v) 1458 (vi) 768 the smallest whole number by which it should be multiplied so as to get a perfect square number and the square root of the square number so obtained are as follows: (i) 7; √1764 = 42 (ii) 5; √900 = 30 (iii) 7; √7056 = 84 (iv) 3; √6084 = 78 (v) 2; √2916 = 54 and (vi) 3; √2304 = 48

---

☛ Related Questions:

• The students of Class VIII of a school donated ₹ 2401 in all for the Prime Minister’s National Relief Fund. Each student donated as many rupees as the number of students in the class. Find the number of students in the class.
• 2025 plants are to be planted in a garden in such a way that each row contains as many plants as the number of rows. Find the number of rows and the number of plants in each row.
• Find the smallest square number that is divisible by each of the numbers 4, 9 and 10.
• Find the smallest square number that is divisible by each of the numbers 8, 15 and 20.